练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为x元（x为正整数），每个月的销售利润为y元．

    （1）当每件商品的售价是多少元时，每个月的利润刚好是2250元？

    （2）当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    （1）65或85；（2）当售价定为75时，每个月可获得最大利润，最大的月利润是2450元． 【解析】试题分析：（1）如果每件商品的售价每上涨1元，则每个月少卖2件，可得销售量为100﹣2（x﹣60），销售量乘以利润即可得到等式[100﹣2（x﹣60）]（x﹣40）=2250，解答即可； （2）将（1）中的2250换成y即可解答． 试题解析：【解析】 （1）[100﹣2（x﹣60...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级（下）期末数学试卷 题型：解答题

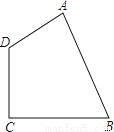
    如图，是一块四边形绿地的示意图，其中AB长为24米，BC长15米，CD长为20米，DA长7米，∠C=90°，求绿地ABCD的面积．

    绿地ABCD的面积为234平方米． 【解析】试题分析：连接BD，先根据勾股定理求出BD的长，再由勾股定理的逆定理判定△ABD为直角三角形，则四边形ABCD的面积=直角△BCD的面积+直角△ABD的面积． 试题解析： 连接BD．如图所示： ∵∠C=90°，BC=15米，CD=20米， ∴BD===25（米）； 在△ABD中，∵BD=25米，AB=24米，DA=7米...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：解答题

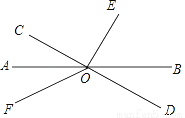
    如图，若直线AB与直线CD交于点O，OA平分∠COF，OE⊥CD．

    (1)写出图中与∠EOB互余的角；

    (2)若∠AOF=30°，求∠BOE和∠DOF的度数．

    （1）∠COA，∠FOA，∠BOD；（2）60°. 【解析】试题分析：（1）由于OA平分∠COF和∠COA与∠BOD是对顶角，得到∠COA=∠FOA=∠BOD，根据垂直定义有∠EOB+∠BOD=90°，根据互为余角的定义即可得到结论；（2）由（1）知∠COA=∠FOA=∠BOD=30°，由平角的意义可求得∠DOF，根据垂直定义可求得∠BOE． （1）【解析】 ∵OA平分∠COF， ∴...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：单选题

    有理数m，n在数轴上的位置如图所示，则化简│n│-│m-n│的结果是（ ）

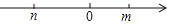
    A. m B. 2n-m C. -m D. m-2n

    C 【解析】根据数轴的特点，可知n＜0＜m，且|n|＞|m|，因此可知m-n＞0，所以根据绝对值的意义可知│n│-│m-n│=-n-m+n=-m. 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：单选题

    下列各组数中，相等的是（ ）

    A. –1与（–4）+（–3） B. 与–（–3）

    C. 与 D. 与–16

    B 【解析】本题考查有理数的比较大小,先利用有理数的加法,绝对值,有理数的乘方进行,然后再进行比较,可以选出正确的答案.

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：填空题

    在平面直角坐标系中，将抛物线C1：y=x2绕点（1，0）旋转180°后，得到抛物线C2，定义抛物线C1和C2上位于﹣2≤x≤2范围内的部分为图象C3．若一次函数y=kx+k﹣1（k＞0）的图象与图象C3有两个交点，则k的范围是：__．

    ﹣2+2＜k≤或≤k≤﹣4+6或k≥15 【解析】试题解析：如图,由题意图象的解析式为 图象是图中两根红线之间的上的部分图象. 由,则A(2,4),B(?2,?16),D(2,0). 因为一次函数y=kx+k?1(k>0)的图象与图象有两个交点 当直线经过点A时,满足条件,4=2k+k?1,解得 ②当直线与抛物线相切时,由 消去y得到 ∵△=0， 解得或 ...

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：单选题

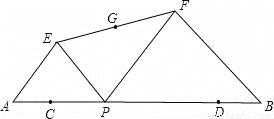
    如图，已知AB=12，点C，D在AB上，且AC=DB=2，点P从点C沿线段CD向点D运动（运动到点D停止），以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF，连接EF，取EF的中点G，下列说法中正确的有（　　）

    ①△EFP的外接圆的圆心为点G；②四边形AEFB的面积不变；

    ③EF的中点G移动的路径长为4；④△EFP的面积的最小值为8．

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】试题解析：如图，分别延长AE、BF交于点H. ∵等腰Rt△APE和等腰Rt△PBF， ∴, . ∴四边形EPFH为平行四边形， ∴EF与HP互相平分. ∵G为EF的中点， ∴G也为PH中点， 即在P的运动过程中，G始终为PH的中点， ∴G的运行轨迹为△HCD的中位线MN. ∵CD=12?2?2=8， ∴MN=4，即G的移...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    计算：

    （1）（﹣a2）3•4a （2）2x（x+1）+（x+1）2．

    (1)-4a7; (2) 3x2+4x+1． 【解析】试题分析:（1）根据幂的乘方、同底数幂的乘法进行计算即可； （2）根据单项式乘以多项式以及完全平方公式进行计算即可． 【解析】 （1）原式=﹣a6•4a =﹣4a7； （2）原式=2x2+2x+x2+2x+1 =3x2+4x+1．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省平凉市中考数学模拟试卷 题型：解答题

    如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）

    （1）求抛物线的解析式和点A的坐标；

    （2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；

    （3）如图2，已知直线y=x﹣分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

    （1）A点坐标为（﹣3，0）；（2）；P点坐标为（， ）；（3）以QD为腰的等腰三角形的面积最大值为． 【解析】试题分析：（1）把B点的坐标代入抛物线的解析式，求出a的值即可，令y=0，解方程求得x的值，即可得点A的坐标；（2）当点P在x轴上方时，连接AP交y轴于点B′，可证△OBP≌△OB′P，可求得B′坐标，利用待定系数法可求得直线AP的解析式，联立直线y=x，可求得P点坐标；当点P在x...

    查看答案和解析>>

    同步练习册答案