练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：

    （1）（﹣a2）3•4a （2）2x（x+1）+（x+1）2．

    (1)-4a7; (2) 3x2+4x+1． 【解析】试题分析:（1）根据幂的乘方、同底数幂的乘法进行计算即可； （2）根据单项式乘以多项式以及完全平方公式进行计算即可． 【解析】 （1）原式=﹣a6•4a =﹣4a7； （2）原式=2x2+2x+x2+2x+1 =3x2+4x+1．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省武汉市中考数学模拟试卷二 题型：填空题

    某产品包装上标明重量是150g±3g，说明其重量在_____g至_____g之间为合格品．

    147 153 【解析】根据题意得，150+3=153，150-3=147. 故答案为(1). 147 (2). 153

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：解答题

    某商品的进价为每件40元，售价为每件60元时，每个月可卖出100件；如果每件商品的售价每上涨1元，则每个月少卖2件．设每件商品的售价为x元（x为正整数），每个月的销售利润为y元．

    （1）当每件商品的售价是多少元时，每个月的利润刚好是2250元？

    （2）当每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

    （1）65或85；（2）当售价定为75时，每个月可获得最大利润，最大的月利润是2450元． 【解析】试题分析：（1）如果每件商品的售价每上涨1元，则每个月少卖2件，可得销售量为100﹣2（x﹣60），销售量乘以利润即可得到等式[100﹣2（x﹣60）]（x﹣40）=2250，解答即可； （2）将（1）中的2250换成y即可解答． 试题解析：【解析】 （1）[100﹣2（x﹣60...

    查看答案和解析>>

    科目：初中数学 来源：四川省南充市营山县城南二小2017-2018学年上学期九年级数学期末质量检测试卷 题型：单选题

    下列图形中，是中心对称图形的是（　　）

    A. B. C. D.

    C 【解析】试题解析：根据中心对称图形的定义，只有C是中心对称图形. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：解答题

    如图，在△ABC中，AB=AC，∠A=36°，DE是AC的垂直平分线．

    （1）求证：△BCD是等腰三角形；

    （2）△BCD的周长是a，BC=b，求△ACD的周长（用含a，b的代数式表示）

    （1）见解析；（2）a﹣b+b+b=a+b． 【解析】试题分析:（1）先由AB=AC，∠A=36°，可求∠B=∠ACB==72°，然后由DE是AC的垂直平分线，可得AD=DC，进而可得∠ACD=∠A=36°，然后根据外角的性质可求：∠CDB=∠ACD+∠A=72°，根据等角对等边可得：CD=CB，进而可证△BCD是等腰三角形； （2）由（1）知：AD=CD=CB=b，由△BCD的周长是...

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：填空题

    若一个三角形三个内角的度数之比为1：2：3，则这个三角形中的最大的角度是 ．

    90° 【解析】 试题分析：已知三角形三个内角的度数之比，可以设一份为k，根据三角形的内角和等于180°列方程求三个内角的度数，从而确定三角形的最大角的度数． 【解析】 设三个内角的度数分别为k，2k，3k． 则k+2k+3k=180°， 解得k=30°， 则2k=60°，3k=90°， 这个三角形最大的角等于90°． 故答案为：90°．

    查看答案和解析>>

    科目：初中数学 来源：北京八十五中2017-2018学年上期期末八年级数学试卷 题型：单选题

    一个多边形每个外角都等于36°，则这个多边形是几边形（ ）

    A．7 B．8 C．9 D．10

    D 【解析】 试题分析：多边形的外角和是360°，又有多边形的每个外角都等于36°，所以可以求出多边形外角的个数，进而得到多边形的边数． 【解析】 这个多边形的边数是：=10．故答案是D．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

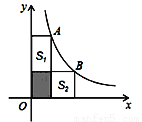
    如图，点A、B在函数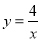（x＞0）的图象上，过点A、B分别向x、y轴作垂线，若阴影部分图形的面积恰好等于S1，则S1+S2=__________．

    4 【解析】∵S1=S阴影，S2+S阴影=4， ∴S1+S2=4.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省定安县中考数学仿真试卷（二） 题型：解答题

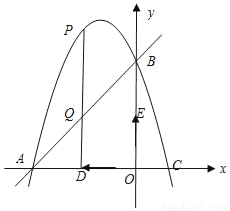
    如图，抛物线经过点A（﹣3，0）、B（0，3），C（1，0）．

    （1）求抛物线及直线AB的函数关系式；

    （2）有两动点D、E同时从O出发，以每秒1个单位长度的相同的速度分别沿线段OA、OB向A、B做匀速运动，过D作PD⊥OA分别交抛物线和直线AB于P、Q，设运动时间为t（0＜t＜3）．

    ①求线段PQ的长度的最大值；

    ②连接PE，当t为何值时，四边形DOEP是正方形；

    ③连接DE，在运动过程中，是否存在这样的t值，使PE=DE？若存在，请求出t的值；若不存在，请说明理由．

    （1）y=﹣x2﹣2x+3；y=x+3；（2）①当t=1时，PQ的长度有最大值，最大值为4；②当t为时，四边形DOEP是正方形；③存在．当t=时，PE=DE 【解析】试题分析：（1）已知了抛物线上的三个点的坐标和直线上两个点的坐标，直接利用待定系数法即可求出抛物线和直线的解析式；（2）①用t表示出线段PQ的长，利用二次函数的性质即可求解；②OE=OD=PD时，四边形四边形DOEP是正方形，由...

    查看答案和解析>>

    同步练习册答案