
分别从一个几何体的正面、左面、上面观察得到的平面图形如图所示,则这个几何体是( )
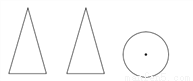
A. 圆柱 B. 圆锥 C. 球 D. 棱柱
B 【解析】A选项, 圆柱体分别从一个几何体的正面,左面,上面观察得到的平面图形是:矩形,矩形,圆形,所以不符合题意,B选项,圆锥体分别从一个几何体的正面,左面,上面观察得到的平面图形是:等腰三角形,等腰三角形,圆形,符合题意,C选项,球体分别从一个几何体的正面,左面,上面观察得到的平面图形是:圆形,圆形,圆形,D选项,棱柱体分别从一个几何体的正面,左面,上面观察得到的平面图形是:矩形,矩形...科目:初中数学 来源:广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型:填空题
方程x2=2x的解为____________.
x1=0,x2=2 【解析】试题分析:先移项得到x2﹣2x=0,再把方程左边进行因式分解得到x(x﹣2)=0,方程转化为两个一元一次方程:x=0或x﹣2=0,即可得到原方程的解为x1=0,x2=2. 【解析】 ∵x2﹣2x=0, ∴x(x﹣2)=0, ∴x=0或x﹣2=0, ∴x1=0,x2=2. 故答案为x1=0,x2=2.查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学全册综合测试一 题型:单选题
如图是一个正方体,则它的表面展开图可以是( )
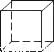
A.  B.
B. 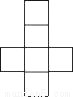 C.
C.  D.
D. 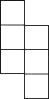
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:填空题
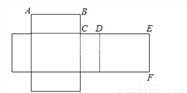
如图,某长方体的表面展开图的面积为430,其中BC=5,EF=10,则AB=________ .
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:单选题
下列平面图形中不能围成正方体的是( )
A. 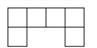 B.
B. 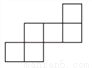 C.
C. 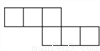 D.
D. 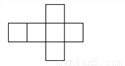
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第13章 轴对称 单元测试卷 题型:填空题
如图,树AB垂直于地面,为测树高,小明在C处测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,则计算出树的高度是__________米.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第13章 轴对称 单元测试卷 题型:单选题
平面直角坐标系中,点(﹣2,4)关于x轴的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
C 【解析】 试题分析:利用关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,﹣y),进而得出答案. 【解析】 点(﹣2,4)关于x轴的对称点为;(﹣2,﹣4), 故(﹣2,﹣4)在第三象限. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省九年级(上)期末数学试卷 题型:填空题
分解因式:3ax2 6axy+3ay2=_________________;
6axy+3ay2=_________________;
查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版七年级数学下册 5.3 平行线的性质 同步练习 题型:解答题
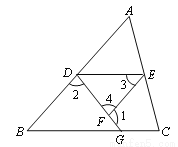
如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
【解析】
∵∠1+∠2=180o(已知)
又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
见解析 【解析】试题分析:根据同角的补角可证: ∠2=∠4,再根据内错角相等,两直线平行可证得: AB∥EF , 根据两直线平行,内错角相等可得:∠3=∠ADE,等量代换可得∠ADE=∠B , 再利用同位角相等两直线平行可得: DE∥BC,利用两直线平行,同旁内角互补可得:∠DEC+∠C =180°. 试题解析:∵∠1+∠2=180°(已知), 又∵∠1+ ∠4 =180°...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com