
如图,B是线段AD上一点,C是线段BD的中点.
(1)若AD=8,BC=3,求线段CD,AB的长;
(2)试说明:AD+AB=2AC.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:解答题
已知在同一内有三点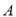 、
、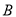 、
、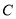 ,请你根据下列要求用直尺和圆规作图:
,请你根据下列要求用直尺和圆规作图:
①画线段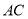 ,
, 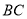 .
.
②作射线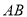 ,并在射线
,并在射线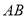 上取一点
上取一点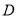 ,使
,使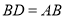 .
.
③作射线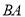 ,并在射线
,并在射线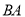 上取一点
上取一点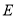 ,使
,使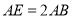 .
.
请根据以上作图,解答下列问题:
(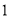 )请问
)请问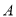 、
、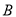 分别是哪两条线段的中点?并说理由.
分别是哪两条线段的中点?并说理由.
( )若巳知线段
)若巳知线段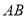 的长为
的长为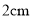 ,求线段
,求线段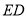 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:单选题
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
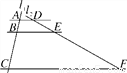
A. 4 B. 5 C. 6 D. 8
C 【解析】已知AD∥BE∥CF,根据平行线分线段成比例定理可得,即,解得EF=6,故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:单选题
在下列单项式中,与2xy是同类项的是( )
A. 2x2y2 B. 3y C. xy D. 4x
C 【解析】试题分析:根据同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,同类项与字母的顺序无关,与系数无关. 【解析】 与2xy是同类项的是xy. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:单选题
下面计算正确的是( )
A. 3x2-x2=3 B. 3a2+2a3=5a5
C. 3+x=3x D. -0.75ab+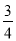 ba=0
ba=0
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:填空题
往返于甲、乙两地的客车,中途停靠3个车站(来回票价一样), 且任意两站间的票价都不同,共有____种不同的票价,需准备____种车票.
10 20 【解析】途中有三个车站,加上两端的终点站共五个车站. 以A、B、C、D、E表示五个车站,需要不同的票价的车票可以表示为AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种, 因为往返的车票虽然票价一样,但方向不同, 所以至多要准备10×2=20种不同的车票.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
若∠1=40.4°,∠2=40°4′,则∠1与∠2的关系是( )
A、∠1=∠2 B、∠1>∠2 C、∠1<∠2 D、以上都不对
B 【解析】 试题分析:根据角度的换算关系1°=60′,因此0.4°=24′,所以∠1>∠2. 故选B查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:填空题
某商店将彩电按成本价提高50%,然后在广告上写“大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电成本价是___________.
1350. 【解析】 试题分析:根据利润=售价-成本价,设每台彩电成本价是x元,列方程求解即可. 试题解析:设每台彩电成本价是x元, 依题意得:(50%•x+x)×0.8-x=270, 解得:x=1350.查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(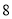 分)如图,在四边形
分)如图,在四边形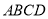 中,
中, 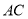 平分
平分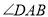 ,
, 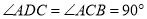 ,
, 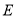 为
为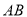 的中点,连接
的中点,连接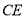 、
、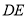 ,
, 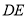 交
交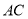 于点
于点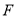 .
.
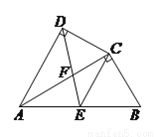
( )求证:
)求证: 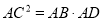 .
.
(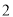 )若
)若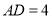 ,
, 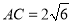 ,求
,求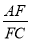 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com