
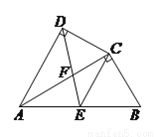
(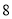 分)如图,在四边形
分)如图,在四边形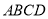 中,
中, 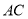 平分
平分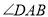 ,
, 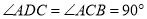 ,
,  为
为 的中点,连接
的中点,连接 、
、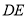 ,
, 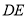 交
交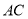 于点
于点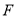 .
.
(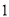 )求证:
)求证: 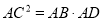 .
.
(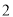 )若
)若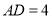 ,
, 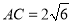 ,求
,求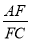 的值.
的值.
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:填空题
如图,B是线段AD上一点,C是线段BD的中点.
(1)若AD=8,BC=3,求线段CD,AB的长;
(2)试说明:AD+AB=2AC.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:单选题
下列不是一元一次方程的( )
A. 5x+3=3x﹣7 B. 1+2x=3 C. 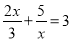 D. x﹣7=0
D. x﹣7=0
查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:单选题
如图,DE是ΔABC的中位线,则ΔADE与ΔABC的面积之比是为( )
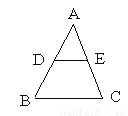
A. 1:1 B. 1:2 C. 1:3 D. 1:4
D 【解析】试题分析:由中位线可知DE∥BC,且DE=BC;可得△ADE∽△ABC,相似比为1:2,根据相似三角形的面积比是相似比的平方,可得△ADE∽△ABC的面积比为1:4. 故选D查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:填空题
已知 (x、y、z均不为零),则
(x、y、z均不为零),则 _____________.
_____________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
(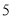 分)如图,一次函数
分)如图,一次函数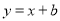 的图象与反比例函数
的图象与反比例函数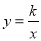 图象交于
图象交于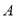 ,
, 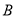 两点,点
两点,点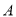 的坐标为
的坐标为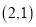 .
.
( )求一次函数和反比例函数的表达式.
)求一次函数和反比例函数的表达式.
(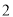 )求
)求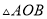 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:填空题
若关于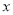 的一元二次方程
的一元二次方程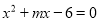 有一个根为
有一个根为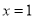 ,则另一个根为__________.
,则另一个根为__________.
查看答案和解析>>
科目:初中数学 来源:人教版九年级年级数学下册第二十九章 达标检测卷 题型:填空题
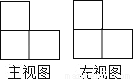
下图是由四个相同的小正方体组成的立体图形的主视图和左视图,那么原立体图形可能是_____.(把下图中正确的立体图形的序号都填在横线上)
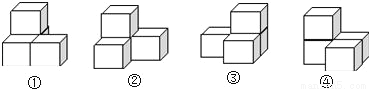
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:解答题
已知:如图,∠1=120°,∠C=60°,判断AB与CD是否平行?为什么?
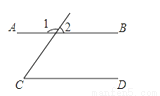
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com