
正方形的一条对角线长为4,则这个正方形面积是( )
A. 8 B. 4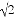 C. 8
C. 8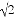 D. 16
D. 16
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
平行四边形的两条邻边的比为2:1,周长为60cm,则这个四边形较短的边长为________.
10cm 【解析】设较短边长为xcm,则相邻的边长为2xcm,由题意则有 2(2x+x)=60, 解得:x=10, 故答案为:10cm.查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
当太阳斜照或直照时,一个放在水平地面上的长方形状的箱子在地面上留下的影子是_____.
矩形,五边形或六边形 【解析】当太阳斜照或直射时,一个放在水平地面上的长方形状的箱子在地面上留下的影子是矩形,无边形或六边形.查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
如图,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)请写出图中两对全等的三角形;
(2)求证:四边形BCEF是平行四边形.
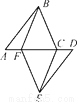
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图1,测得AC=2,当∠B=60°时,如图2,AC=( )
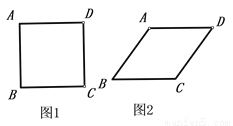
A. 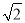 B. 2 C.
B. 2 C. 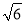 D. 2
D. 2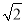
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
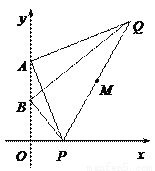
如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
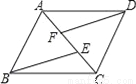
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C. 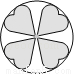 D.
D. 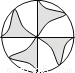
查看答案和解析>>
科目:初中数学 来源:北师大版七年级上册数学全册综合测试卷 题型:单选题
下列四个有理数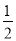 、0、1、-2,任取两个相乘,积最小为 ( )
、0、1、-2,任取两个相乘,积最小为 ( )
A. 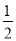 B. 0 C. -1 D. -2
B. 0 C. -1 D. -2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com