练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

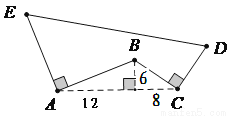
    如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，求图中实线所围成的图形的面积S．

    200． 【解析】试题分析： 如图，过点E作EF⊥AC于点F，过点 D作DH⊥AC于点H，由已知条件分别证△EFA≌△ABG和△BGC≌△DHC，即可得到EF=AG=12，FA=BG=6，CH=BG=6，DH=CG=8，由此可得FH=FA+AG+GC+CH=32，这样即由S梯形EFDH-S△AEF-S△ABC-S△DHC即可求得所求图形的面积了. 试题解析： ∵AE⊥AB且...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省广州市越秀区2016-2017学年八年级下册数学期末考试试卷 题型：解答题

    如图，在平面直角坐标系中，直线y=kx+b经过点A（﹣30，0）和点B（0，15），直线y=x+5与直线y=kx+b相交于点P，与y轴交于点C．

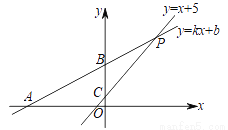
    （1）求直线y=kx+b的解析式．

    （2）求△PBC的面积．

    （1）y=x+15；（2）100． 【解析】试题分析：（1）将点A和点B的坐标代入直线的解析式得到关于k、b的方程组，从而可求得k、b的值，于是可得到直线AB的解析式； （2）联立两直线解析式成方程组，通过解方程组可得出点P的坐标，由一次函数图象上点的坐标特征可求出点C的坐标，进而可得出线段BC的长度，最后利用三角形的面积公式求解即可. 试题解析：（1）将点A（﹣30，0）、B（...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳市襄城区2016-2017学年度上学期期末考试七年级数学试卷 题型：单选题

    数轴上的点A到原点的距离是3，则点A表示的数为（ ）

    A. 3或﹣3 B. 6 C. ﹣6 D. 6或﹣6

    A 【解析】试题分析：设这个数是x，则|x|=3，解得x=+3或﹣3．故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（北师大版）：期中检测题 题型：单选题

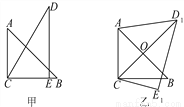
    将一副三角板如图甲摆放，∠A＝45°，∠D＝30°，斜边AB＝6，DC＝7，把△DCE绕点C顺时针旋转15°得到△D1CE1(如图乙)，此时AB与CD1交于点O，则线段AD1的长为( )

    A. 3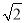 B. 5 C. 4 D.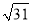

    B 【解析】【解析】 ∵∠ACB=∠DEC=90°，∠D=30°，∴∠DCE=90°﹣30°=60°，∴∠ACD=90°﹣60°=30°．∵旋转角为15°，∴∠ACD1=30°+15°=45°．又∵∠A=45°，∴△ACO是等腰直角三角形，∴AO=CO=AB=×6=3，AB⊥CO．∵DC=7，∴D1C=DC=7，∴D1O=7﹣3=4．在Rt△AOD1中，AD1===5．故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（北师大版）：期中检测题 题型：单选题

    不等式组的解集是( )

    A. x≥－3 B. －3≤x＜4 C. －3≤x＜2 D. x＞4

    B 【解析】【解析】 解不等式2x+9≥3，得：x≥﹣3，解不等式＞x﹣1，得：x＜4，∴不等式组的解集为﹣3≤x＜4，故选B．

    查看答案和解析>>

    科目：初中数学 来源：重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型：解答题

    计算：（1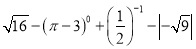） （2）

    （1）2；（2）7. 【解析】试题分析： （1）结合“零指数幂的意义”、“负整数指数幂的意义”及“数的开方”进行计算即可； （2）先按“幂的相关运算法则”计算，再合并同类项即可. 试题解析： （1）原式=； （2）原式=.

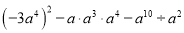
    查看答案和解析>>

    科目：初中数学 来源：重庆市校2017-2018学年八年级上学期第二阶段考试数学试卷 题型：单选题

    如图，有一个形如六边形的点阵，它的中心是一个点，作为第一层，第二层每边有两个点，第三 层每边有三个点，依次类推，如果n层六边形点阵的总点数为331，则n等于（ ）

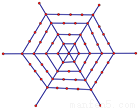
    A. n=6 B. n=8 C. n=11 D. n=13

    C 【解析】观察图形，由题意可得： 第一层的点的个数为：1个； 第二层的点的个数为：6=1×6（个）； 第三层的点的个数为：6+6=2×6（个）； 第四层的点的个数为：6+6+6=3×6（个）； ……； 第n层的点的个数为：(n-1)×6（个），其中且n为整数； ∴前n层的点的总个数为： 由解得（不合题意，舍去）. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期中检测题 题型：解答题

    解方程： .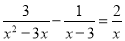

    无解 【解析】试题分析：方程两边同乘以x（x-3），化为整式方程，解答即可． 试题解析：【解析】 两边同乘x(x－3)，得3－x＝2x－6， 解得x＝3， 经检验，x＝3是原分式方程的增根， ∴原方程无解．

    查看答案和解析>>

    科目：初中数学 来源：湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考（12月）数学试卷 题型：解答题

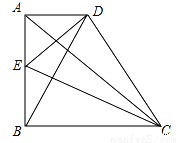
    如图所示，在直角梯形ABCD中，∠ABC=90°，AD∥BC，AB=BC，E是AB的中点，CE⊥BD

    （1）求证：BE=AD；

    （2）求证：AC是线段ED的垂直平分线；

    （3）△DBC是等腰三角形吗?并说明理由

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）利用已知条件证明△BAD≌△CBE(ASA)，根据全等三角形的对应边相等即可得到结论； （2）证明AD=AE，根据线段垂直平分线的逆定理即可解答； （3）由△DAB≌△EBC，得到DB=EC，又由△AEC≌△ADC，得到EC=DC，所以DB=DC，即可解答． 试题解析：【解析】 (1)∵∠ABC＝90°，BD⊥...

    查看答案和解析>>

    同步练习册答案