
请你写出一个含有字母m,n的单项式,使它的系数为﹣2,次数为3.可列式为_____.
﹣2mn2 【解析】试题解析:含有字母m,n的单项式,使它的系数为-2,次数为3.可列式为-2mn2. 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:解答题
已知,点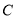 是线段
是线段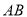 所在平面内任意一点,分别以
所在平面内任意一点,分别以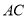 、
、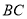 为边,在
为边,在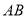 同侧作等边
同侧作等边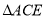 和等边
和等边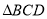 ,联结
,联结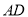 、
、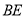 交于点
交于点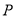 .
.
(1)如图1,当点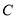 在线段
在线段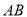 上移动时,线段
上移动时,线段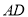 与
与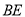 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点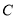 在直线
在直线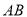 外,且
外,且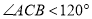 ,仍分别以
,仍分别以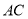 、
、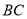 为边,在
为边,在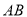 同侧作等边
同侧作等边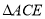 和等边
和等边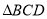 ,联结
,联结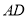 、
、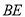 交于点
交于点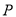 .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时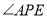 是否随
是否随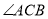 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出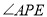 的度数;
的度数;
(3)如图3,在(2)的条件下,联结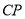 ,求证:
,求证: 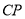 平分
平分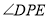 .
.

查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:填空题
神舟飞船绕地球飞行一周约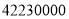 米,这个数用科学记数法表示是__________米
米,这个数用科学记数法表示是__________米
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:解答题
先化简,再求值
(1)(x+2)2﹣(x+5)(x﹣5),其中x=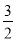 .
.
(2)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y=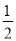 .
.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:填空题
(﹣x﹣3)_____=9﹣x2.
(x+3) 【解析】试题解析:∵-(x+3)=-x-3 ∴(-x-3)(x+3)=9-x2. 故横线上应填写:(x+3).查看答案和解析>>
科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:单选题
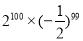 =
=
A、2 B、-2 C、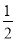 D、-
D、-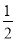
查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:解答题
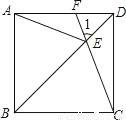
如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.
(1)求证:△ABE∽△FDE;
(2)当BE=3DE时,求tan∠1的值.
查看答案和解析>>
科目:初中数学 来源:2017年海南省文昌市中考数学模拟试卷 题型:单选题
由四舍五入法得到的近似数8.8×103,下列说法中正确的是( )
A. 精确到十分位,有2个有效数字
B. 精确到个位,有2个有效数字
C. 精确到百位,有2个有效数字
D. 精确到千位,有4个有效数字
C 【解析】试题分析:有效数字是指从左边开始第一个不是零的数字开始,一直到最右边的数字为止,数字总共的个数有几个,则有效数字就有几个;精确度首先将近似数转化成原数,然后看近似数中最后一位在什么位上,则精确到哪一位.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
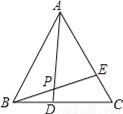
如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是_____度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com