
如图,直线a∥b,直线c是截线,如果∠1=50°,那么∠2等于( )
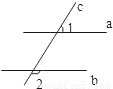
A. 150° B. 140° C. 130° D. 120°
C 【解析】【解析】 ∵∠1=50°, ∴∠1的邻补角是130°, ∵a∥b, ∴∠2=130°(两直线平行,同位角相等),故选C. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:解答题
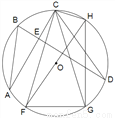
如图,在⊙O中,两条弦AC,BD垂直相交于点E,等腰△CFG内接于⊙O,FH为⊙O直径,且AB=6,CD=8.
(1)求⊙ 的半径;
的半径;
(2)若CF=CG=9,求图中四边形CFGH的面积.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:单选题
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=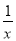 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=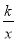 的图象上,则k的值为( )
的图象上,则k的值为( )
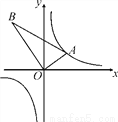
A. -4 B. 4 C. -2 D. 2
A 【解析】试题解析:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D. 设点A的坐标是(m,n),则AC=n,OC=m, ∵∠AOB=90°, ∴∠AOC+∠BOD=90°, ∵∠DBO+∠BOD=90°, ∴∠DBO=∠AOC, ∵∠BDO=∠ACO=90°, ∴△BDO∽△OCA, ∴, ∵OB=2OA, ∴BD=2m,OD=...查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:解答题
(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,(___________)
∵AB∥CD,EF∥AB
∴EF∥CD(___________)
∴∠D=________(___________)
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.________
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D=________
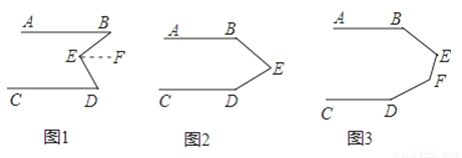
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型:单选题
下列各组角中,∠1与∠2是对顶角的为( )
A. 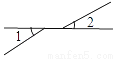 B.
B. 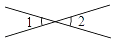 C.
C. 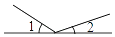 D.
D. 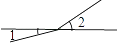
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型:解答题
下表是佳佳往表妹家打长途电话的收费记录:
时间/min | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
电话费/元 | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)若佳佳的通话时间是10 min,则需要付多少电话费?
(1)反映了电话费与通话时间之间的关系;其中通话时间是自变量,电话费是因变量. (2)需付6元电话费. 【解析】分析:(1)根据函数的定义可知,通话时间是自变量,电话费是因变量; (2)观察图表中的数据,1分钟0.6,两分钟1.2,相差0.6,可知成等差数列,从而求解. 本题解析: (1)通话时间与电话费;其中通话时间是自变量,电话费是因变量; (2)设时间为x...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型:单选题
A,B两地相距20 km,甲、乙两人都从A地去B地,如图,l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系,下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )
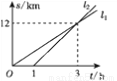
A. 1 B. 2 C. 3 D. 4
C 【解析】①l2与x轴的交点是(1,0),因此可得乙晚出发1小时。故①项正确。 ②l1和l2的交点坐标为(3,12),因此可得乙出发3-1=2小时后追上甲。故②项错误。 ③项,甲的速度等于12÷3=4千米/小时。故③项正确。 ④项,从图象中可得,甲、乙在12千米处相遇,而乙的速度更快,因此乙将会先到达B地。故④项正确。 综上所述,正确的说法有①③④,共3个。 ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 全册综合测试卷 题型:填空题
若x,y满足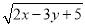 +(2x+3y-13)2=0,则2x-y的值为________.
+(2x+3y-13)2=0,则2x-y的值为________.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型:解答题
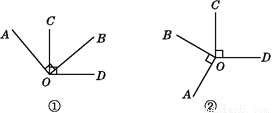
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com