练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果3x2y3与xm＋1yn－1的和仍是单项式，则（n－3m）2016的值为____.

    1 【解析】∵3x2y3与xm＋1yn－1的和仍是单项式， ∴m+1=2,n-1=3, ∴m=1,n=4, ∴（n－3m）2016=（4－3）2016=1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十六章达标检测卷 题型：填空题

    当1＜x＜4时，|x－4|＋＝________________．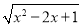

    3 【解析】试题解析：∵1＜x＜4 ∴x-1>0,x-4<0 ∴|x－4|＋=｜x-4｜+｜x-1|=4-x+x-1=3.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型：单选题

    如图所示,将△ABC沿BC方向平移2 cm得到△DEF,若△ABC的周长为16 cm,则四边形ABFD的周长为 (　　)

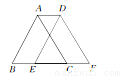
    A. 16 cm B. 18 cm C. 20 cm D. 22 cm

    C 【解析】试题分析：由平移的性质可知，DF=AC，AD=CF=3cm，∴四边形ＡＢＦＤ的周长＝AB+BF+DF+AD＝AB+BC+AC+AD+CF，∵AB+BC+AC＝１４ｃｍ，∴四边形ABFD的周长="20cm" ; 故选C．

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型：单选题

    如果代数式3x2-6的值为21，则x的值为（ ）

    A. 3 B. ±3 C. -3 D. ±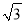

    B 【解析】【解析】 根据题意得：3x2﹣6=21，即x2=9，解得：x=±3，故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第2章 整式的加减 单元测试卷 题型：解答题

    （8分）先化简再求值：

    （1）－9y＋6x2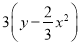＋，其中x＝2，y＝－1；

    （2）2a2b－[2a2＋2（a2b＋2ab2）]，其中a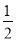＝，b＝1.

    （1）22；（2） 【解析】试题分析：本题考查了整式的化简求值，先把整式去括号合并同类项，然后再所给字母的值代入，按照有理数运算的顺序计算，代入求值时要补上省去的括号和乘号. 解：(1)原式＝－9y＋6x2＋3y－2x2＝4x2－6y. 当x＝2，y＝－1时，原式＝4×22－6×(－1)＝22. (2)原式＝2a2b－(2a2＋2a2b＋4ab2)＝2a2b－2a2－2a2...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第2章 整式的加减 单元测试卷 题型：单选题

    如图所示，三角尺的面积为（　　）

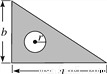
    A. ab－r2 B. 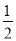ab－r2 C. 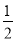ab－πr2 D. ab

    C 【解析】∵三角尺的面积=三角形的面积-圆的面积， ∴三角尺的面积= ab－πr2. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第2章 整式的加减 单元测试卷 题型：单选题

    甲、乙、丙三家超市为了促销一种定价相同的商品，甲超市先降价20%，后又降价10%；乙超市连续两次降价15%；丙超市一次降价30%．那么顾客到哪家超市购买这种商品更合算（ ）

    A. 甲 B. 乙 C. 丙 D. 一样

    C 【解析】试题分析：设商品原价为x，表示出三家超市降价后的价格，然后比较即可得出答案． 【解析】 设商品原价为x， 甲超市的售价为：x（1﹣20%）（1﹣10%）=0.72x； 乙超市售价为：x（1﹣15%）2=0.7225x； 丙超市售价为：x（1﹣30%）=70%x=0.7x； 故到丙超市合算． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：期末达标检测卷 题型：填空题

    =___________。

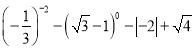    8 【解析】根据负整指数幂、零次幂的性质、绝对值、算术平方根计算即可得=9-1-2+2=8. 故答案为：8.

    查看答案和解析>>

    科目：初中数学 来源：福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型：解答题

    某商场销售一批名牌衬衫，平均每天可售出20件，每件赢利30元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．

    （1）若商场平均每天赢利750元，每件衬衫应降价多少元？

    （2）每件衬衫降价多少元时，商场平均每天赢利最多？

    （1）为了尽快减少库存，应减价15元；（2）降价10元时，利润最大为800元. 【解析】试题分析：（1）每天盈利=每件盈利×销售件数，每件实际盈利=原每件盈利-每件降价数．检验时，要考虑尽快减少库存，就是要保证盈利不变的情况下，降价越多，销售量越多，达到减少库存的目的． （2）在（1）的基础上，由特殊到一般，列出二次函数，求出二次函数的最大值． 试题解析：【解析】 （1）设每件...

    查看答案和解析>>

    同步练习册答案