练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    数轴上到表示-2的点的距离是3的点所表示的数是 .

    -5和1 【解析】试题分析：依题意知，数轴上与-2点距离为3的情况有两种，当该点在-2点的左边时，该点为-2-3=-5.当该点在2的右边是，则-2+3=1。所以答案为-5和1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省遂宁市2017-2018学年七年级（上）月考数学试卷 题型：单选题

    在数轴上，与表示数﹣1的点的距离是2的点表示的数是（　　）

    A. 1 B. 3 C. ±2 D. 1或﹣3

    D 【解析】该点可以在-1的左边或右边，则有-1-2=-3；-1+2=1． 故选D

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：填空题

    设甲、乙两车在同一直线公路上匀速行驶，开始时甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车上的货物转给甲车，然后甲车继续前行，乙车向原地返回、．设xs后两车间的距离为ym，y与x的函数关系如图所示，则乙车的速度是_______m/s．

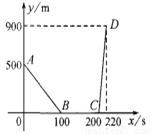
    25. 【解析】【解析】 设甲车的速度是a米/秒，乙车的速度为b米/秒，由题意，得： ，解得： ．故答案为：25．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：单选题

    下列说法正确的是（ ）

    A. 4的平方根是±2 B. 8的立方根是±2 C. 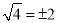D.

    A 【解析】解：A．4的平方根是±2，故本选项正确； B．8的立方根是2，故本选项错误； C． =2，故本选项错误； D． =2，故本选项错误； 故选A．

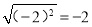
    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：解答题

    计算： （1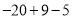） （2）

    （1）-16；（2）0. 【解析】分析：（1）根据有理数加减运算法则计算即可；（2）根据有理数混合运算顺序和运算法则计算即可． 本题解析： (1)原式=?11?5=?16； (2)原式=?1?×[2?9]=?1+1=0.

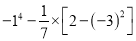
    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：单选题

    若有理数a、b满足ab＞0，且a＋b＜0，则下列说法正确的是（　　）

    A. a、b可能一正一负 B. a、b都是正数

    C. a、b都是负数 D. a、b中可能有一个为0

    C 【解析】试题分析：有理数a、b满足ab＞0，则a，b同号，又因为a+b＜0，所以a，b同为负数，故选：C.

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

    如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD、BC于E、F，作BH⊥AF于点H，分别交AC、CD于点G、P，连结GE、GF．

    （1）求证：△OAE≌△OBG．

    （2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由．

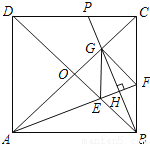
    （1）证明见解析；（2）菱形. 【解析】试题分析： （1）这两个三角形有一条直角边相等，一个直角相等只需证还有一条边相等即可； （2）先证AF是BG的垂直平分线，再分别求出∠BEF和∠BFE的度数. 试题解析： （1）证明：∵四边形ABCD是正方形，∴OA=OB，∠AOE=∠BOG=90°． ∵BH⊥AF，∴∠AHG=∠AHB=90°，∴∠GAH+∠AGH=90...

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：单选题

    如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（　　）

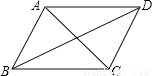
    A. 当AB=BC时，四边形ABCD是菱形

    B. 当AC⊥BD时，四边形ABCD是菱形

    C. 当∠ABC=90°时，四边形ABCD是矩形

    D. 当AC=BD时，四边形ABCD是正方形

    D 【解析】A.因为有一组邻边相等的平行四边形叫做菱形，所以A正确； B.因为对角线相等的平行四边形是菱形，所以B正确； C.因为有一个角是直角的平行四边形是矩形，所以C正确； D.对角线相等的平行四边形是矩形，不一定是正方形，所以D错误. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：单选题

    如图，△ABC的两个顶点BC均在第一象限，以点（0，1）为位似中心，在y轴左方作△ABC的位似图形△AB′C′，△ABC与△A′B′C的位似比为1：2．若设点C的纵坐标是m，则其对应点C′的纵坐标是（）

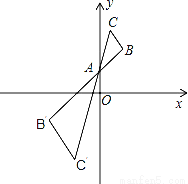
    A． ﹣（2m﹣3） B． ﹣（2m﹣2） C． ﹣（2m﹣1） D． ﹣2m

    A． 【解析】 试题分析：设点C的纵坐标为m，则A、C间的纵坐标的长度为（m-1），∵△ABC放大到原来的2倍得到△A′B′C， ∴C′、A间的纵坐标的长度为2（m-1）， ∴点C′的纵坐标是-[2（m-1）-1]=-（2m-3）． 故选：A． 考点:1.位似变换,2.坐标与图形性质.

    查看答案和解析>>

    同步练习册答案