练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若有理数a、b满足ab＞0，且a＋b＜0，则下列说法正确的是（　　）

    A. a、b可能一正一负 B. a、b都是正数

    C. a、b都是负数 D. a、b中可能有一个为0

    C 【解析】试题分析：有理数a、b满足ab＞0，则a，b同号，又因为a+b＜0，所以a，b同为负数，故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省遂宁市2017-2018学年七年级（上）月考数学试卷 题型：单选题

    一天早晨的气温是﹣7℃，中午上升了11℃，晚上又下降了9℃，晚上的气温是（　　）

    A. ﹣5℃ B. ﹣6℃ C. ﹣7℃ D. ﹣8℃

    A 【解析】试题解析：晚上的气温是 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年广东省八年级12月月考数学试卷 题型：填空题

    已知方程组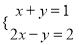的解为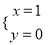，则一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为_____．

    （1, 0） 【解析】【解析】 ∵方程组的解为，∴一次函数y=﹣x+1和y=2x﹣2的图象的交点坐标为（1，0）．故答案为：（1，0）．

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：解答题

    已知A-2B=7a2-7ab，且B=-4a2+6ab+7．

    （1）用含a、b的代数式表示A.

    （2）若|a+1|+(b-2)2=0，求A 的值．

    （1）A=；（2）A=3. 【解析】分析：（1）表示出A，然后去掉括号，再根据整式的加减运算方法进行计算即可得解；（2）根据非负数的性质列式求出a、b的值，然后代入进行计算即可得解． 本题解析： (1)∵A?2B=7a²?7ab， ∴A=7a²?7ab+2B,=7a²?7ab+2(?4a²+6ab+7)=7a²?7ab?8a²+12ab+14=?a²+5ab+14， ...

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：填空题

    数轴上到表示-2的点的距离是3的点所表示的数是 .

    -5和1 【解析】试题分析：依题意知，数轴上与-2点距离为3的情况有两种，当该点在-2点的左边时，该点为-2-3=-5.当该点在2的右边是，则-2+3=1。所以答案为-5和1.

    查看答案和解析>>

    科目：初中数学 来源：浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型：单选题

    下列各式① m；② x+5=7 ；③ 2x+3y；④ m＞3 ；⑤ 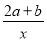中,整式的个数有 （ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】①m是整式，故本项正确； ②x+5=7是等式，不是整式，故本项错误； ③2x+3y是整式，故本项正确； ④m>3是不等式，不是整式，故本项错误； ⑤分母中含有字母不是整式，故本项错误； 综上可得①③正确，共2个。 故选B.

    查看答案和解析>>

    科目：初中数学 来源：九年级数学第一学期1.3.2正方形的判定 同步练习 题型：解答题

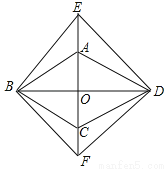
    如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．

    （1）求证：△BAE≌△BCF；

    （2）若∠ABC=40°，则当∠EBA=　 时，四边形BFDE是正方形．

    （1）证明见解析；（2）25. 【解析】分析：（1）由菱形的性质得出AB=CB，由等腰三角形的性质得出∠BAC=∠BCA，证出∠BAE=∠BCF，由SAS证明△BAE≌△BCF即可；（2）由菱形的性质得出AC⊥BD，OA=OC，OB=OD，∠ABO=∠ABC=20°，证出OE=OF，得出四边形BFDE是菱形，证明△OBE是等腰直角三角形，得出OB=OE，BD=EF，证出四边形BFDE是矩形，...

    查看答案和解析>>

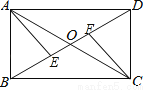
    科目：初中数学 来源：初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型：解答题

    如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．

    （1）求证：AE=CF；

    （2）若AB=6，∠COD=60°，求矩形ABCD的面积．

    【解析】试题分析：（1）由矩形的性质得出OA=OC，OB=OD，AC=BD，∠ABC=90°，证出OE=OF，由SAS证明△AOE≌△COF，即可得出AE=CF； （2）证出△AOB是等边三角形，得出OA=AB=6，AC=2OA=12，在Rt△ABC中，由勾股定理求出BC的长，即可得出矩形ABCD的面积． 试题解析：（1）证明：∵四边形ABCD是矩形，∴OA=OC，OB=OD，AC=B...

    查看答案和解析>>

    科目：初中数学 来源：河北省沙河市2017-2018学年九年级上学期期末模拟联考数学试卷(冀教版) 题型：单选题

    如图，AB是⊙O的直径，若∠BDC=40°，则∠AOC的度数为（　　）

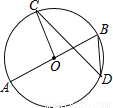
    A． 80° B． 100° C． 140° D． 无法确定

    B. 【解析】 试题分析：根据同弧所对圆心角是圆周角的2倍，先求得∠BOC=2∠BDC=80°，再进一步求得∠AOC的度数． ∵∠BOC=2∠BDC=80°， ∴∠AOC=180°-∠BOC =180°-80° =100°． 故选：B． 考点:圆周角定理.

    查看答案和解析>>

    同步练习册答案