
��ͼ�������ı��ι���ֱ��l�Գƣ���C=90�㣬��д��a��b�ij��ȣ��������G�Ķ�����
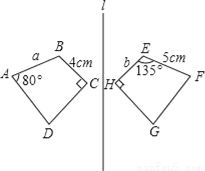
 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ��Ӫ�кӿ���2017��2018ѧ��ȵ�һѧ����ĩ�������꼶��ѧ�Ծ� ���ͣ������
���㣺 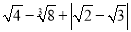 =______��
=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
����x�ķ���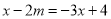 ��
��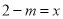 �Ľ⻥Ϊ�෴����
�Ľ⻥Ϊ�෴����
��1����m��ֵ��
��2�������������̵Ľ⣮
��1����2�� �������������������1���������һ�����̵Ľ⣬Ȼ����ݻ�Ϊ�෴���ĺ͵���0��ʽ�õ����ڵķ��̣��ٸ���һԪһ�η��̵Ľⷨ��⼴�ɣ� ��2���ѵ�ֵ�����������̵Ľ���㼴�ɣ� �����������1���ɵã� �������У� ����ã� ��2���ɣ���÷��̵Ľ�Ϊ����÷��̵Ľ�Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�й������ġ�һ��һ·�����轫�ٽ��ҹ�����������Ļ������������ݹ滮����һ��һ·�������������˿�ԼΪ4400000000�ˣ�������ÿ�ѧ��������ʾΪ�� ��
A. 44��108 B. 4.4��109 C. 4.4��108 D. 4.4��1010
B ����������ѧ�������ı�ʾ��ʽΪa��10n����ʽ������1��|a|��10��nΪ������ȷ��n��ֵʱ��Ҫ����ԭ�����aʱ��С�����ƶ��˶���λ��n�ľ���ֵ��С�����ƶ���λ����ͬ����ԭ������ֵ��1ʱ��n����������ԭ���ľ���ֵ��1ʱ��n�Ǹ����� �������� 4 400 000 000=4.4��109�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��Դ�ж�����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ��С���������м�λ�ã���A�������ÿ��6m����ת60�㣬��֪AB=BC=6m��
��1��С���Ƿ�����A�㣬���ܻص�A�㣬������m���߹���·����һ��ʲôͼ�Σ�Ϊʲô����·��A��B��C������
��2��������ͼ�ε��ڽǺͣ�
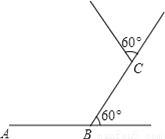
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��Դ�ж�����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪��A��x��4�����B��3��y������y��Գƣ���ôx+y��ֵΪ____________.
1 ���������������� �ߵ�A��x��4�����B��3��y������y��Գƣ���x=��3��y=4����x+y=����3��+4=1�� �ʴ�Ϊ��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��Դ�ж�����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
AD�ǡ�ABC�Ľ�ƽ�����ҽ�BC��D������D��DE��AB��E��DF��AC��F,�����н��۲�һ����ȷ���ǣ� ��
A��DE=DF B��BD =CD C��AE=AF D����ADE=��ADF
B �������� ���������������֪��AD�ǽ�ƽ���ߣ������н�ƽ���ߵ��ý����ߵľ�����ȣ�������DE=DF����Ϊ������ADE��ADF��ֱ�������Σ���AD�ǹ����ߣ�������������ADE��������ADFȫ�ȣ�����AE=AF ,��ADE=��ADF ֻ��ѡ��B���жϣ���ѡB�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ��������Ϫ��2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
���⡰ȫ�������εĶ�Ӧ����ȡ����������ǣ�_____________
��Ӧ����ȵ�����������ȫ�� �����������ȷ��������ǣ�����������ȫ�ȣ������ǣ���Ӧ����ȣ�����������ۻ������ɵõ������⣬Ȼ���ж����ɣ� �������� ��ȫ�������εĶ�Ӧ����ȡ��������ǣ�����������ȫ�ȣ������ǣ���Ӧ����ȣ�����������ǣ���Ӧ����ȵ�������ȫ�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�������������̳�����2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��֪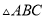 ��
�� 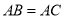 ��
�� 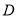 Ϊ
Ϊ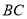 ��һ�㣬
��һ�㣬 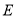 Ϊ
Ϊ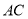 ��һ�㣬
��һ�㣬 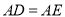 ��
��
��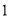 �����
�����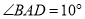 ��
�� 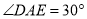 ����ô
����ô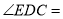 __________
__________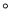 ��
��
��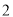 �����
�����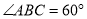 ��
�� 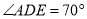 ����ô
����ô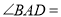 __________
__________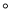 ��
�� 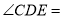 __________
__________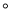 ��
��
��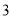 ����
����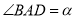 ��
�� 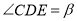 ����
����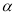 ��
�� 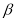 ֮��Ĺ�ϵʽ����˵�����ɣ�
֮��Ĺ�ϵʽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com