
某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元,可售出180个,定价每增加1元,销售量将减少10个;定价每减少1元,销售量将增加10个.因受库存影响,每批进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
该商品每个定价为60元,进货100个. 【解析】利用销售利润=售价﹣进价,根据题中条件可以列出利润与x的关系式,求出即可. 【解析】 设每个商品的定价是x元, 由题意,得(x﹣40)[180﹣10(x﹣52)]=2000, 整理,得x2﹣110x+3000=0, 解得x1=50,x2=60. 当x=50时,进货180﹣10(50﹣52)=200个>180个,不...科目:初中数学 来源:青海省2018届九年级上学期12月月考数学试卷 题型:解答题
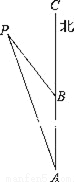
如图,一艘轮船早上8时从点A向正北方向出发,小岛P在轮船的北偏西15°方向,轮船每小时航行15海里,11时轮船到达点B处,小岛P此时在轮船的北偏西30°方向.
(1)求此时轮船距小岛为多少海里?
(2)在小岛P的周围20海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市临武县景山学校中考数学模拟试卷 题型:单选题
某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
人数(人) | 1 | 3 | 4 | 1 |
分数(分) | 80 | 85 | 90 | 95 |
那么这9名学生所得分数的众数和中位数分别是( )
A. 90,90 B. 90,85 C. 90,87.5 D. 85,85
A 【解析】在这一组数据中90是出现次数最多的,故众数是90; 排序后处于中间位置的那个数是90,那么由中位数的定义可知,这组数据的中位数是90; 故选:A.查看答案和解析>>
科目:初中数学 来源:山东省潍坊高新技术产业开发区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
单项式﹣3πxy2z3的系数和次数分别是( )
A. ﹣3π,5 B. ﹣3,6 C. ﹣3π,7 D. ﹣3π,6
D 【解析】单项式﹣3πxy2z3的系数是﹣3π和次数分别是6.所以选D.查看答案和解析>>
科目:初中数学 来源:山东省潍坊高新技术产业开发区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
两个不为零的有理数相除,如果交换它们的位置,商不变,那么( )
A. 两数相等 B. 两数互为相反数 C. 两数互为倒数 D. 两数相等或互为相反数
D 【解析】【解析】 交换它们的位置,商不变则两数相等或互为相反数,故选D.查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(九) 题型:填空题
比较大小: 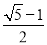 _____1(填“<”或“>”或“=”).
_____1(填“<”或“>”或“=”).
查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(九) 题型:单选题
一只不透明的袋子中装有两个完全相同的小球,上面分别标有1,2两个数字,若随机地从中摸出一个小球,记下号码后放回,再随机摸出一个小球,则两次摸出小球的号码之积为偶数的概率是( )
A. 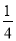 B.
B. 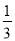 C.
C. 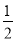 D.
D. 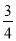
查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄石市中考数学模拟试卷 题型:填空题
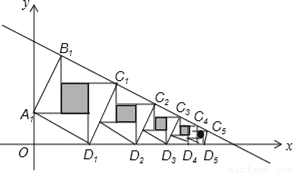
赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣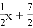 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
查看答案和解析>>
科目:初中数学 来源:广东省2017年中考数学一模试卷 题型:解答题
如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
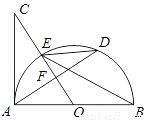
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
(1)AD=3;(2)证明见解析;(3)AC= 【解析】试题分析:(1)由垂径定理可得AF=DF,要求AD的长度,即要求AF的长度,由∠EBA=30°可以得出∠FOA=60°,进而得出∠FAO=30°,已知OA的长度结合30°余弦值,不难求出AF的长度,即可求出AD的长度;(2)要证∠BED=∠C即要证明∠DAB=∠C,由于∠C+∠CAF=90°,∠DAB+∠CAF=90°,不难证明;(3)...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com