练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    两道单选题都含有A、B、C、D四个选择支，瞎猜这两道题恰好全部猜对的概率有（ ）

    A. B. C. D.

    D 【解析】.选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型：单选题

    若等腰三角形腰长为10cm，底边长为16 cm,那么它的面积为( )

    A、48 cm2 B、36 cm2 C、24 cm2 D、12 cm2

    A 【解析】 试题分析：如图所示：AB=AC=10cm，BC=16cm；根据等腰三角形的三线合一定理可得：BD=CD=8cm，根据勾股定理可得：AD=6cm，则三角形的面积=16×6÷2=48.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：解答题

    已知一个圆的半径为6cm,这个圆的内接正六边形的周长和面积各是多少?

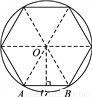
    54． 【解析】试题分析：连接圆心和六边形的顶点，将六边形分成六个全等的三角形，这六个三角形是等边三角形.所以正六边形的边长是6cm,所以周长就是36cm；计算每个三角形面积，过圆心作一个三角形的高，求得高是3所以一个三角形的面积是9cm2,故正六边形的面积是54cm2. 如图所示,⊙O 中内接正六边形,OA＝6cm． ∵正六边形内接于⊙O，∴中心角∠AOB＝60°， ∴△...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第24章小结与复习 练习 题型：单选题

    如图,A、B、C 是⊙O 上三点,∠ACB＝25°,则∠BAO 的度数是( )

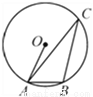
    A. 55° ； B. 60°； C. 65°； D. 70°；

    C 【解析】试题分析：连接OB，要求∠BAO的度数，只要在等腰三角形OAB中求得一个角的度数即可得到答案，利用同弧所对的圆周角是圆心角的一半可得∠AOB=50°，然后根据等腰三角形两底角相等和三角形内角和定理即可求得． 【解析】 连接OB， ∵∠ACB=25°， ∴∠AOB=2×25°=50°， 由OA=OB， ∴∠BAO=∠ABO， ∴∠BAO=（18...

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试2 题型：解答题

    质量检查员准备从一批产品中抽取10件进行检查，如果是随机抽取，为了保证每件产品被检的机会均等；

    （1）请采用计算器模拟实验的方法，帮质量检查员抽取被检产品；

    （2）如果没有计算器，你能用什么方法抽取被检产品？

    （1）利用计算器模拟产生随机数与这批产品编号相对应，产生10个号码即可．（2）利用摸球或抽签等 【解析】试题分析： （1）利用计算器模拟产生随机数（2）利用摸球或抽签等． 试题解析： （1）利用计算器模拟产生随机数与这批产品编号相对应，产生10个号码即可． （2）利用摸球或抽签等．

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试2 题型：填空题

    对某名牌衬衫抽检结果如下表：

    抽检件数

    10

    20

    100

    150

    200

    300

    不合格件数

    0

    1

    3

    4

    6

    9

    如果销售1000件该名牌衬衫，至少要准备____件合格品，供顾客更换

    30 【解析】.

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试2 题型：解答题

    一张圆桌旁有四个座位，A先坐在如图所示的座位上，B、C、D三人随机坐到其他三个座位上．求A与B不相邻而坐的概率．

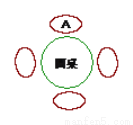
    【解析】试题分析：概率的求法：概率=所求情况数与所有情况数的比. 由于A的位置已经确定，B、C、D随机而坐的情况共有6种（如图所示）： 6种情况出现的可能性相同．其中A与B不相邻而坐的情况共有2种，所以所求概率是：P=．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（1）练习 题型：填空题

    如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，则弦AB的长为_______cm．

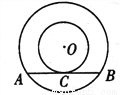
    16 【解析】设切点是C，连接OA，OC．则在Rt△OAC中，AC==8cm，所以AB=16cm．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（2）测试 题型：填空题

    如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是______．

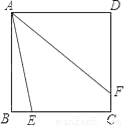
    BE+DF=EF 【解析】如图,延长CD到M,使DM=BE, 连接AM,EF, ∵四边形ABCD为正方形, ∴∠B=∠ADC=90°,AB=AD, 在△ABE与△ADM中, , ∴△ABE≌△ADM（SAS）, ∴∠BAE=∠DAM,AE=AM, ∴∠BAE+∠DAF=∠DAM+∠DAF=∠MAF, ∵∠EAF=45°, ∴∠EAF...

    查看答案和解析>>

    同步练习册答案