
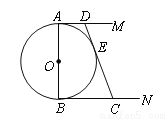
如图,⊙O 的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设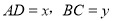 .
.
(1)求证: 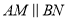 ;(2)求
;(2)求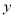 关于
关于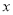 的关系式.
的关系式.
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:解答题
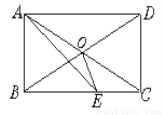
如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)练习 题型:解答题
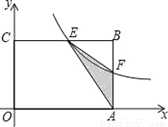
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 25.1.1随机事件 测试 题型:填空题
小明和小华在做抛骰子游戏,规则是这样的:抛出去的骰子落地后,朝上的点数是偶数,则小明获胜,否则小华获胜,那么这个游戏是____(填“公平”或“不公平”)的.
公平 【解析】∵骰子的点数分别为:1,2,3,4,5,6, ∴点数是偶数的有:2,4,6,点数是奇数的有:1,3,5, ∴P(小明获胜)= =,P(小华获胜)= =, ∴P(小明获胜)=P(小华获胜), ∴这个游戏公平. 故答案为:公平.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
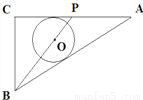
如图,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:解答题
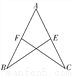
如图所示,AB=AC,F,E分别是AB,AC的中点.求证:△ABE≌△ACF.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
下列条件中,能判定两个直角三角形全等的是( )
A. 一锐角对应相等 B. 两锐角对应相等
C. 一条边对应相等 D. 两条直角边对应相等
D 【解析】试题分析:三角形全等可以利用SAS、SSS、ASA和AAS来进行判定,直角三角形还可以用HL定理来进行判定.本题中D选项可以利用SAS来进行判定三角形全等.查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是________°.
15 【解析】因为∠A=50°,AB=AC,所以∠ABC=60°. 因为DE垂直平分AB,所以DA=DB,所以∠DBA=∠A=50°. 所以∠DBC=65°-50°=15°. 故答案为15.查看答案和解析>>
科目:初中数学 来源:2017北师大版数学八年级上册 第4章 一次函数 单元检测题 题型:解答题
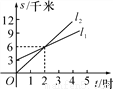
已知A地在B地正南方向 3 千米处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地的距离S (千米)与所行时间t (时)之间的关系如图,其l2表示甲运动 的过程,l1表示乙运动的过程,根据图象回答:
(1)甲和乙哪一个在A 地,哪一个在B 地?
(2)追者用多长时间追上被追者?哪一个是追者?
(3)求出表示甲、乙的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com