
在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是________°.
15 【解析】因为∠A=50°,AB=AC,所以∠ABC=60°. 因为DE垂直平分AB,所以DA=DB,所以∠DBA=∠A=50°. 所以∠DBC=65°-50°=15°. 故答案为15. 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:单选题
直线y=x与抛物线y=-2x2的交点是()
A. (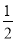 ,0) B. (
,0) B. (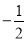 ,
, 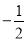 ) C. (
) C. (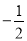 ,
, 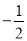 ),(0,0) D. (0,0)
),(0,0) D. (0,0)
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(3)练习 题型:解答题
如图,⊙O 的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设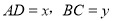 .
.
(1)求证: 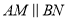 ;(2)求
;(2)求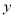 关于
关于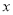 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册 第十二章 全等三角形 12.2 三角形全等的判定 同步练习题 含答案 题型:单选题
如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
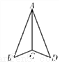
A. 120° B. 125° C. 127° D. 104°
C 【解析】试题分析:AB=AD,CB=CD,AC=AC所以∆ABC?∆ACD,所以∠B=∠D=30°,因为∠BAD=46°,所以∠CAD=23°,所以∠ACD=180°-30°-23°=127°,故选C.查看答案和解析>>
科目:初中数学 来源:数学人教版八年级上册13.4课题学习 最短路径问题同步练习题 题型:解答题
有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.
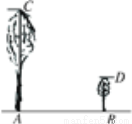
查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,∠ABC=50°,AD垂直且平分BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
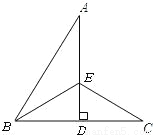
A. 50° B. 25° C. 80° D. 115°
D 【解析】因为AD垂直且平分BC,所以EB=EC,所以∠EBC=∠C. 因为BE平分∠ABC,所以∠ABC=2∠EBC=50°,所以∠EBC=25°,所以∠C=25°. 所以∠AEC=∠C+∠EDC=25°+90°=115°. 故选D.查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,AC=AD,BC=BD,则有( )
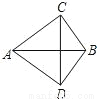
A. AB垂直平分CD B. CD垂直平分AB
C. AB与CD互相垂直平分 D. CD平分∠ACB
A 【解析】试题分析:因为AC=AD,BC=BD,所以点A和点B在线段CD的垂直平分线上,即AB垂直平分CD,故选;A.查看答案和解析>>
科目:初中数学 来源:安徽省濉溪县2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
已知4x2mym+n与-3x6y2是同类项,则m-n=________
4 【解析】试题解析:由题意可知, ,解得 ,所以 .查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(2)练习 题型:解答题
如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.
(1)求∠AEC的度数;(2)求证:四边形OBEC是菱形.
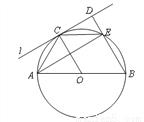
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com