练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    代数式的家中来了几位客人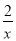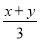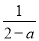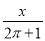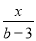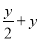： ， ， ， ， ， ，其中属于分式家族成员的有（ 　）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】【解析】 分式有： ， ， ，共3个，故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省泰州市医药高新区2017-2018学年七年级上学期第二次月考（12月）数学试卷 题型：填空题

    若m-n=-1，则(m-n)2-2m+2n==__________.

    3 【解析】因为m-n=-1， 所以(m-n)2-2m+2n=(m-n)2-2(m-n)=(m-n)(m-n-2)=3.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年山东省临沂市沂水县七年级（上）期中数学试卷 题型：单选题

    下列各组单项式中，不是同类项的一组是（　　）

    A. x2y和2xy2 B. ﹣32和3 C. 3xy和﹣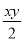 D. 5x2y和﹣2yx2

    A 【解析】根据同类项的定义中相同字母的指数也相同，分别判断各选项即可得解． 【解析】 A、相同字母的指数不相同，不是同类项； B、符合同类项的定义，是同类项． C和D所含字母相同且相同字母的指数也相同的项是同类项， 故选A． “点睛”本题考查同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，注意同类项定义中的两个“相同”：（1）所含字母相同，（2）相同字...

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市2017-2018学年八年级12月月考数学试卷 题型：填空题

    如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，BD=8cm，那么CD=_________．

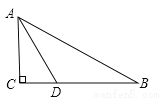
    4cm． 【解析】【解析】 作DE⊥AB于E．∵∠B=30°，DE⊥AB，∴DE=BD=4cm．∵AD平分∠CAB，DE⊥AB，∠C=90°，∴CD=DE，∴CD=4cm，故答案为：4 cm．

    查看答案和解析>>

    科目：初中数学 来源：广东省江门市2017-2018学年八年级12月月考数学试卷 题型：单选题

    如图，AE∥BF，∠E=∠F，下列添加的条件不能使△ADE≌△BCF的是（　　）

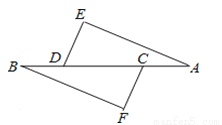
    A. ∠ADE=∠BCF B. DE=CF C. AE=BF D. BD=AC

    A 【解析】【解析】 A．加条件∠ADE=∠BCF，不能证明△ADE≌△BCF，故此选项正确； B．加条件DE=CF，可以用AAS证明△ADE≌△BCF，故此选项错误； C．加条件AE=BF，可以用ASA证明△ADE≌△BCF，故此选项错误； D．由BD=AC可以得到CB=DA，再有两角对应相等，可以使△ADE≌△BCF，故此选项错误； 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型：解答题

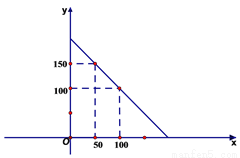
    某超市老板到批发中心选购甲、乙两种品牌的水杯。甲进货单价为3元、乙进货单价为4元；考虑各种因素，预计购进乙品牌水杯的数量y（个）与甲品牌水杯的数量x（个）之间的函数关系如图所示．

    （1）根据图象，求y与x之间的函数关系式；

    （2）若该超市每销售1个甲水杯可获利0.5元，每销售1个乙水杯可获利1元。请写出获利W（元）与x（个）的函数关系式；

    （3）在（2）的条件下，超市老板决定用不超过700元购进甲、乙两种品牌的水杯，且这两种品牌的水杯全部售出后获利不低于149元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？

    （1）y=-x+200；（2）W=-0.5x+200；（3） 当甲100时最大利润=150元. 【解析】试题分析：（1）根据函数图象由待定系数法就可以直接求出与之间的函数关系式； （2）1个甲水杯可获利0.5元，每销售1个乙水杯可获利1元，从而得到获利与的函数关系式. （3）设甲品牌进货个，则乙品牌的进货个，根据条件建立不等式组求出其解即可． 试题解析：（1）设与之间的函数关系...

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型：解答题

    计算与求值：

    （1）计算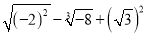： （2）求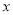的值：(x＋1)2 =16

    （1）7；（2）x=3 或x=－5 【解析】试题分析：根据平方根立方根的定义进行运算即可. 试题解析：（1）原式 （2） 或 或

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：解答题

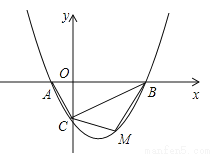
    如图，抛物线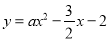（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．

    （1）求抛物线的解析式；

    （2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；

    （3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．

    （1）；（2）（，0）；（3）4，M（2，﹣3）． 【解析】试题分析：方法一： （1）该函数解析式只有一个待定系数，只需将B点坐标代入解析式中即可． （2）首先根据抛物线的解析式确定A点坐标，然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置，由此确定圆心坐标． （3）△MBC的面积可由S△MBC=BC×h表示，若要它的面积最大，需要使h取最大值，即点M到直线BC...

    查看答案和解析>>

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：解答题

    如图，将长方形ABCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点E．

    （1）试判断△BDE的形状，并说明理由；

    （2）若AB=4，AD=8，求△BDE的面积．

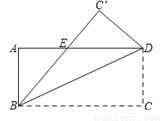
    【答案】（1）△BDE是等腰三角形；（2）10．

    【解析】试题分析：（1）由折叠可知，∠CBD=∠EBD，再由AD∥BC，得到∠CBD=∠EDB，即可得到∠EBD=∠EDB，于是得到BE=DE，等腰三角形即可证明；

    （2）设DE=x，则BE=x，AE=8﹣x，在Rt△ABE中，由勾股定理求出x的值，再由三角形的面积公式求出面积的值．

    【解析】
    （1）△BDE是等腰三角形．

    由折叠可知，∠CBD=∠EBD，

    ∵AD∥BC，

    ∴∠CBD=∠EDB，

    ∴∠EBD=∠EDB，

    ∴BE=DE，

    即△BDE是等腰三角形；

    （2）设DE=x，则BE=x，AE=8﹣x，

    在Rt△ABE中，由勾股定理得：AB2+AE2=BE2即42+（8﹣x）2=x2，

    解得：x=5，

    所以S△BDE=DE×AB=×5×4=10．

    考点：翻折变换（折叠问题）．

    【题型】解答题
    【结束】
    18

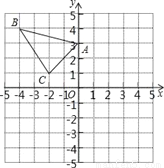
    △ABC在直角坐标系内的位置如图所示．

    （1）分别写出A、B、C的坐标；

    （2）请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称，并写出B1的坐标；

    （3）请在这个坐标系内画出△A2B2C2，使△A2B2C2与△ABC关于原点对称，并写出A2的坐标．

    （1）A（0，3）；B（﹣4，4）；C（﹣2，1）；（2）B1的坐标为：（4，4）；（3）A2（0，﹣3） 【解析】试题分析：（1）根据三角形在平面直角坐标系的位置，分别写出作标点；（2）作关于y轴对称的图形见解析；（3）作关于原点对称图形见解析； 试题解析:（1）根据平面直角坐标系可知点A,B,C的坐标为A(0,3);B(-4,4);C(-2,1)； （2）作图如下图:(4,4...

    查看答案和解析>>

    同步练习册答案