
如图,M为线段AB的中点,C点将线段MB分成MC:CB=1:2的两部分,若MC=2,求线段AB的长.
从(l)、(2)中任选一道小题解答.
(1)认真阅读,理解题意,把解题过程补充完整:

【解析】
因为MC:CB=1:2,MC=2.
所以CB=____
所以MB=____+____=6
因为M是AB中点,
所以AB=____ . MB=____
(2)若你有别的计算方法,也可以独立完成.
(1)4,MC,CB,2,12;(2)见解析. 【解析】试题分析:(1)由MC:CB=1:2,MC=2,可得CB的长,进而求出MB,由M是AB中点, 即可得AB和MB的长; (2)由M是AB中点,可得AB=2 MB,由MC:CB=1:2,MC=2,可得MB=3,MC=6,进而求得AB. 试题解析:(1)因为MC:CB=1:2,MC=2. 所以CB=__4__, ...科目:初中数学 来源:北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型:填空题
计算: 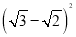 =_______________ .
=_______________ .
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
甲、乙两辆客车分别从相距40千米的A、B两站同时出发,相向而行,相遇时乙车行驶了25千米,如果乙车每小时比甲车多走2千米,求甲、乙两车速度.
甲车的速度是3千米/小时,乙车的速度是5千米/小时. 【解析】试题分析:本题考查了分式方程的应用,根据两车行驶的时间相等列方程求解,解分式方程不要忘记检验. 【解析】 设甲车每小时行驶x千米,乙车每小时行驶(x+2)千米,1分 , , 经检验,x=3是原方程的解且符合题意, x+2=5, 答:甲车的速度是3千米/小时,乙车的速度是5千米/小时. ...查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
计算: 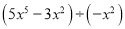 =____________.
=____________.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列等式中,从左到右的变形是因式分解的是( )
A. 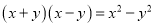 B. 42=2×3×7
B. 42=2×3×7
C. 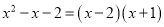 D.
D. 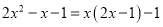
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:解答题
把下列各数在数轴上表示出来,井用“<”连接:-1, 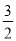 ,|-3| ,0.
,|-3| ,0.
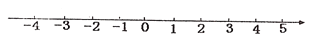
查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:填空题
在数轴上,表示+4的点在原点的____侧,距原点____个单位.
右 4 【解析】由正数在原点右侧,负数在原点左侧,两数到原点的距离即是它们的绝对值,所以在数轴上,表示+4的点在原点的右侧,距原点4个单位. 故答案为:右,4.查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
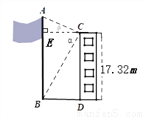
如图,建筑物的高 为17. 32米.在其楼顶
为17. 32米.在其楼顶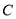 ,测得旗杆底部
,测得旗杆底部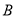 的俯角
的俯角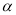 为
为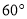 ,旗杆顶部
,旗杆顶部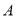 的仰角
的仰角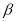 为
为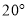 ,请你计算旗杆的高度.(
,请你计算旗杆的高度.(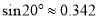 ,
, 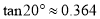 ,
, 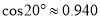 ,
, 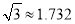 ,结果精确到0.1米)
,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
顺次连结矩形各边中点所得的四边形是( ).
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
B. 【解析】 试题分析:作出图形,根据三角形的中位线定理可得EF=GH=AC,FG=EH=BD,再根据矩形的对角线相等可得AC=BD,从而得到四边形EFGH的四条边都相等,然后根据四条边都相等的四边形是菱形解答. 如图,连接AC、BD ∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点, ∴EF=GH=AC,FG=EH=BD, ∵矩形ABCD...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com