练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解方程：

    （1）1﹣3（x﹣2）=4； （2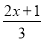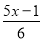）﹣=1．

    （1）x=1，（2）x=﹣3 【解析】试题分析：（1）按照去括号，移项，合并同类项，系数化为1求解；（2）按照去分母，去括号，移项，合并同类项，实数化为1的步骤解答. 【解析】 （1）1﹣3（x﹣2）=4, 1-3x+6=4, -3x=4-6-1, -3x=-3, x=1. （2）﹣=1, 2(2x+1)-(5x-1)=6, 4x+2-5x+...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：贵州省2017-2018学年七年级（上）期中数学试卷 题型：填空题

    比较大小： _____．

    ＞ 【解析】∵， ∴

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省哈尔滨市双城区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    先化简，再求值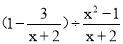． 的值，其中x=2．

    . 【解析】试题分析：先去括号，化除法为乘法进行化简，然后代入求值． 试题解析：原式==， 当时，原式=.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省哈尔滨市双城区2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    已知等腰三角形两边长是8cm和4cm，那么它的周长是（　　）

    A. 12cm B. 16cm C. 16cm或20cm D. 20cm

    D 【解析】【解析】 当腰为4cm时，4+4=8，不能构成三角形，因此这种情况不成立． 当腰为8cm时，8＜8+4，能构成三角形； 此时等腰三角形的周长为8+8+4=20cm． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型：解答题

    旅行社组织了甲、乙两个旅游团到游乐场游玩，两团总报名人数为120人，其中甲团人数不超过50人，游乐场规定一次性购票50人以上可享受团队票．门票价格如下：

    门票类别

    散客票

    团队票A

    团队票B

    购票要求

    超过50人但不超过100人

    超过100人

    票价（元/人）

    80元/人

    70元/人

    60元/人

    旅行社经过计算后发现，如果甲、乙两团合并成一个团队购票可以比分开购票节约300元．

    （1）求甲、乙两团的报名人数；

    （2）当天到达游乐场后发现团队票价格作了临时调整，团队票A每张降价a元，团队票B每张降价2a元，同时乙团队因故缺席了30人，此时甲、乙两团合并成一个团队购票可以比分开购票节约225元，求a的值．

    （1）甲团15人，乙团105人；（2）a=5． 【解析】试题分析：(1)根据甲团队人数为x人,乙团队人数不超过50人,得到x≥70,分两种情况:①当70≤x≤100时,分开购票-甲、乙两团合并成一个团队购票=300元,②当x＞100时,分开购票-甲、乙两团合并成一个团队购票=300元,分别列出方程,即可解答; (2)根据每张门票降价a元,利用甲、乙两团合并成一个团队购票可以比分开购票节...

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型：填空题

    如图，将一副三角板的直角顶点重合，摆放在桌面上，若∠BOC=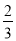∠AOD，则∠AOD=____．

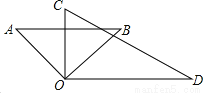
    108 【解析】∵∠AOD=∠AOB+∠COD-∠BOC=180°-∠BOC, ∠BOC=∠AOD， ∴∠AOD=180°-∠AOD， ∴3∠AOD=540°-∠AOD， ∴5∠AOD=540°, ∴∠AOD=108°.

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型：填空题

    已知∠α=60°，则∠α的余角等于____度．

    30 【解析】∵互余两角的和等于90°， ∴α的余角为：90°-60°=30°.

    查看答案和解析>>

    科目：初中数学 来源：吉林省第二实验学校2017-2018学年七年级（上）期中数学试卷 题型：解答题

    计算题：

    （1）（﹣14）﹣（+15）；

    （2）﹣3﹣4+19﹣11+2；

    （3）（﹣4）﹣（﹣1）+（﹣6）+2；

    （4）6÷（-2）+（+3）×；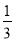

    （5） ．

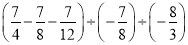    （1）﹣29；（2）3；（3）﹣7；（4）﹣2；（5）． 【解析】试题分析：（1）原式利用减法法则变形，计算即可求出值； （2）原式结合后相加即可求出值； （3）原式利用减法法则变形计算即可求出值； （4）原式先计算乘除运算，再计算加减运算即可求出值； （5）原式利用除法法则变形，计算即可求出值． 试题解析：【解析】 （1）原式=﹣14﹣15=﹣29； ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级下学期模拟考试数学试卷 题型：解答题

    二次函数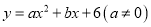的图像交y轴于C点，交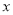轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程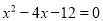的两个根．

    （1）求出点A、点B的坐标及该二次函数表达式．

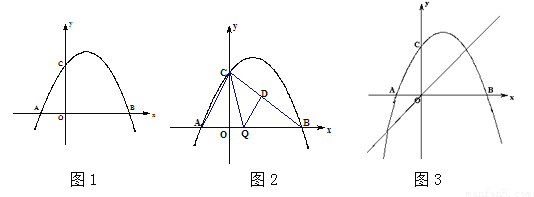
    （2）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．

    （3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且MN=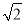，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q．以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出n的值；若不能，请说明理由．

    （1）A（－2，0），B（6，0），；（2）；（3）n=1±或-1±． 【解析】试题分析：（1）解一元二次方程x2-4x-12=0可求A、B两点坐标；将A、B两点坐标代入二次函数y=ax2+bx+6，可求二次函数解析式； （2）由DQ∥AC得△BDQ∽△BCA，利用相似比表示△BDQ的面积，利用三角形面积公式表示△ACQ的面积，根据S△CDQ=S△ABC-S△BDQ-S△ACQ，运用二...

    查看答案和解析>>

    同步练习册答案