
如图,已知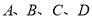 是⊙
是⊙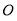 上的四点,延长
上的四点,延长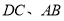 相交于点
相交于点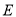 ,若
,若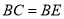 .
.
求证:⊿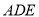 是等腰三角形.
是等腰三角形.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:填空题
方程mx-2y=x+5是二元一次方程时,则m________.
≠1 【解析】先将方程移项整理得: ,由二元一次方程的定义可得: , 解得,故答案为.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
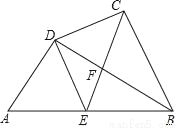
已知:如图,四边形ABCD,∠DCB=90°,对角线BD⊥AD,点E是边AB的中点,CE与BD相交于点F,BD2=AB•BC
(1)求证:BD平分∠ABC;
(2)求证:BE•CF=BC•EF.
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:单选题
已知二次函数y=ax2+bx+c的图象上部分点的横坐标x与纵坐标y的对应值如下表:

那么关于它的图象,下列判断正确的是( )
A. 开口向上 B. 与x轴的另一个交点是(3,0)
C. 与y轴交于负半轴 D. 在直线x=1的左侧部分是下降的
B 【解析】A、由表格知,抛物线的顶点坐标是(1,4).故设抛物线解析式为y=a(x﹣1)2+4. 将(﹣1,0)代入,得 a(﹣1﹣1)2+4=0, 解得a=﹣2. ∵a=﹣2<0, ∴抛物线的开口方向向下, 故本选项错误; B、抛物线与x轴的一个交点为(﹣1,0),对称轴是x=1,则抛物线与x轴的另一个交点是(3,0),故本选项正确; C、...查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
已知关于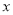 的一元二次方程
的一元二次方程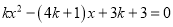 (
(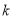 是整数).
是整数).
⑴.求证:方程有两个不相等的实数根;
⑵.若方程的两个实数根分别为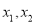 (其中
(其中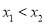 ),设
),设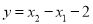 ,判断
,判断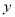 是否为变量
是否为变量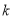 的函数?如果是,请写出函数表达式;若不是,请说明理由.
的函数?如果是,请写出函数表达式;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:填空题
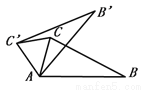
如图,在△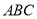 中,
中, 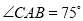 .在同一个平面内,将△
.在同一个平面内,将△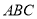 绕点
绕点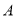 旋转到△
旋转到△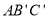 的位置,使得
的位置,使得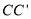 ∥
∥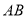 ,则
,则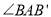 = __________ .
= __________ .
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
如图,△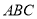 内接于⊙
内接于⊙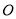 ,
, 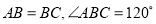 ,
, 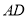 为⊙
为⊙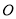 的直径,
的直径, 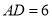 ,那么
,那么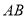 的值为( )
的值为( )

A. 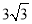 B.
B. 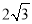 C.
C. 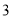 D.
D. 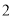
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:填空题
抛物线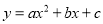 (a>0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,则a的取值范围是____.
(a>0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,则a的取值范围是____.
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:解答题
x为何值时,代数式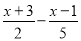 的值是非负数?
的值是非负数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com