练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算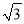：|﹣2|+20150﹣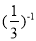+3tan30°．

    0 【解析】试题分析：本题考查了实数的混合运算，根据负数得绝对值等于它的相反数，非零数的零次幂等于1，特殊角的三角函数值计算即可. 原式=2﹣+1﹣3+ =0．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省苏州市2017年中考二模试卷数学试卷 题型：填空题

    若式子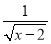在实数范围内有意义，则x的取值范围是　 　．

    x＞2. 【解析】试题分析：使代数式有意义的条件是：分母不能为0，二次根式中的被开方数不能为负数.所以根据题意得：x-2≥0,且x-2≠0.解得：x＞2.故填x＞2.

    查看答案和解析>>

    科目：初中数学 来源：重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型：解答题

    先化简，再求值：

    已知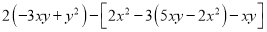，其中x，y满足.

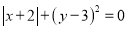    -84. 【解析】试题分析： 首先把原式化简，再由求得，最后代值计算即可. 试题解析： 原式=-6xy+2x2-[2x2-15xy+6x2-xy] =-6xy+2x2-2x2+15xy-6x2+xy =-6x2+10xy ∵ ∴x=-2，y=3， ∴原式=-6+10xy =-6×+10×（-2）×3 =-24-60 =-84．...

    查看答案和解析>>

    科目：初中数学 来源：重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型：单选题

    下面运算正确的是（　　）

    A. 3a+6b=9ab B. 8a4-6a3=2a C. 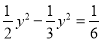D. 3a2b-3ba2=0

    D 【解析】A选项中，因为中两个项不是同类项，不能合并，所以本选项错误； B选项中，因为中两个项不是同类项，不能合并，所以本选项错误； C选项中，因为，所以本选项错误； D选项中， ，所以本选项正确； 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：解答题

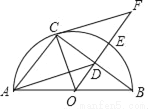
    如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D，点F为OE的延长线上一点且OC2=OD•OF．

    （1）求证：CF为⊙O的切线．

    （2）已知DE=2，tan∠BAC=．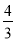

    ①求⊙O的半径；

    ②求sin∠BAD的值．

    （1）证明见解析;（2）①⊙O的半径为5；②sin∠BAD =． 【解析】试题分析：（1）连接OC，利用同圆的半径相等和直径所对的圆周角为直角，得∠OCF=90°，CF是 O的切线；（2）①设 O的半径为r，根据勾股定理列方程解出即可；②过点D作DG⊥OB,利用勾股定理分别求出DG,AG，即可求出sin∠BAD的值. 试题解析： （1），∠COD是公共角 ∴△COD∽△CO...

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：填空题

    关于x的一元二次方程（a﹣1）x2﹣2x+3=0有实数根，则整数a的最大值是_____．

    0 【解析】由题意得： 故整数a的最大值是0.

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省枣庄市中考数学模拟试卷 题型：单选题

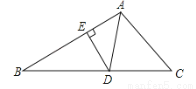
    如图，在△ABC中，AD是角平分线，DE⊥AB于点E，△ABC的面积为15，AB=6，DE=3，则AC的长是( )

    A. 8 B. 6 C. 5 D. 4

    D 【解析】 试题分析：根据角平分线的性质可得：点D到AB和AC的距离相等，根据题意可得：△ABD的面积为9，△ADC的面积为6，则AC的长度=6×2÷3=4.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级（下）期末数学试卷 题型：解答题

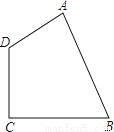
    如图，是一块四边形绿地的示意图，其中AB长为24米，BC长15米，CD长为20米，DA长7米，∠C=90°，求绿地ABCD的面积．

    绿地ABCD的面积为234平方米． 【解析】试题分析：连接BD，先根据勾股定理求出BD的长，再由勾股定理的逆定理判定△ABD为直角三角形，则四边形ABCD的面积=直角△BCD的面积+直角△ABD的面积． 试题解析： 连接BD．如图所示： ∵∠C=90°，BC=15米，CD=20米， ∴BD===25（米）； 在△ABD中，∵BD=25米，AB=24米，DA=7米...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末模拟数学试卷 题型：解答题

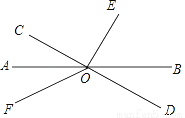
    如图，若直线AB与直线CD交于点O，OA平分∠COF，OE⊥CD．

    (1)写出图中与∠EOB互余的角；

    (2)若∠AOF=30°，求∠BOE和∠DOF的度数．

    （1）∠COA，∠FOA，∠BOD；（2）60°. 【解析】试题分析：（1）由于OA平分∠COF和∠COA与∠BOD是对顶角，得到∠COA=∠FOA=∠BOD，根据垂直定义有∠EOB+∠BOD=90°，根据互为余角的定义即可得到结论；（2）由（1）知∠COA=∠FOA=∠BOD=30°，由平角的意义可求得∠DOF，根据垂直定义可求得∠BOE． （1）【解析】 ∵OA平分∠COF， ∴...

    查看答案和解析>>

    同步练习册答案