
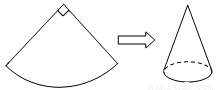
如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 cm.
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
如图直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为( )
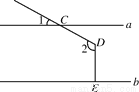
A. 115° B. 125° C. 155° D. 165°
A 【解析】试题分析:过点D作DF∥a,则∠CDF=∠1=25°,∠FDE=90°,则∠2=25°+90°=115°.查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
已知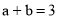 ,
, 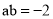 ,则
,则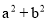 =______.
=______.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2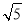 ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
(1)解方程:2x2+4x﹣5=0 (配方法)
(2)解方程:(x﹣3)2+4x(x﹣3)=0.
(1) x=﹣1±;(2) x=3或x=0.6 【解析】试题分析:(1)根据配方法的步骤依次计算可得; (2)用因式分解法求解可得. 试题解析:【解析】 (1)∵2x2+4x=5,∴x2+2x= ,则x2+2x+1=+1,即(x+1)2=,∴x+1=± ,则x=﹣1±; (2)∵(x﹣3)(5x﹣3)=0,∴x﹣3=0或5x﹣3=0,解得:x=3或x=0.6. ...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
一元二次方程x2=2x的根是______.
2或0 【解析】∵x2=2x, ∴x2?2x=0, ∴x(x?2)=0, ∴x=0或x?2=0, ∴一元二次方程x2=2x的根x1=0,x2=2. 故答案为:2或0.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
若x=3是方程x2﹣5x+m=0的一个根,则这个方程的另一个根是( )
A. ﹣2 B. 2 C. ﹣5 D. 5
B 【解析】试题解析:由根与系数的关系,设另一个根为x, 则3+x="5," 即x="2." 故选B.查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:填空题
函数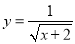 中,自变量x的取值范围是 ;
中,自变量x的取值范围是 ;
查看答案和解析>>
科目:初中数学 来源:江西省2017年秋人教七年级数学上册期末模拟卷 题型:单选题
如图,∠ACB=900,AC=BC,BE⊥CE,AD⊥CE于D,AD=2.5cm,DE=1.7cm,则BE=( )
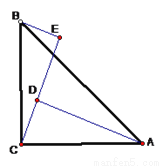
A. 1cm B. 0.8cm C. 4.2cm D. 1.5cm
B 【解析】试题解析: ∵BE⊥CE,AD⊥CE, ∴∠BCE=∠CAD, 在△ACD和△CBE中, ∴△ACD≌△CBE(AAS), ∴AD=CE=2.5cm,BE=CD, ∵CD=CE?DE=2.5?1.7=0.8cm, ∴BE=0.8cm. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com