
已知锐角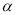 ,满足tan
,满足tan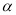 =2,则sin
=2,则sin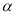 =__________.
=__________.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:单选题
下列各式中,正确的是( )
A. 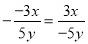 B.
B. 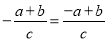
C. 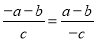 D.
D. 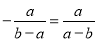
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
已知□ABCD的顶点B(1,1),C(5,1),直线BD,CD的解析式分别是y=kx,y=mx-14,则BC=__________,点A的坐标是_____________.
4 (3,7) 【解析】【解析】 ∵顶点B(1,1),C(5,1),∴BC=5﹣1=4.∵直线BD,CD的解析式分别是y=kx,y=mx﹣14,∴1=k,1=5m﹣14,解得:k=1,m=3,∴直线BD,CD的解析式分别是y=x,y=3x﹣14,∴ ,解得: ,∴D的坐标为:(7,7).∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴A的坐标为:(3,7).故答案为:4,(3,7...查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:解答题
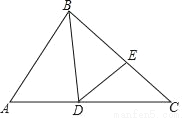
如图,BD是△ABC的角平分线,点E位于边BC上,已知BD是BA与BE的比例中项.
(1)求证:∠CDE=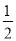 ∠ABC;
∠ABC;
(2)求证:AD•CD=AB•CE.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
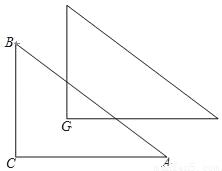
如图,在△ABC中,∠C=90°,BC=6,AC=9,将△ABC平移使其顶点C位于△ABC的重心G处,则平移后所得三角形与原△ABC的重叠部分面积是_____.
查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:单选题
如图,在△ABC中,∠B=80°,∠C=40°,直线l平行于BC.现将直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN与△ABC相似,则旋转角为( )
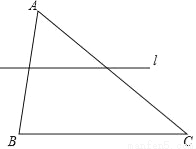
A. 20° B. 40° C. 60° D. 80°
B 【解析】因为旋转后得到△AMN与△ABC相似,则∠AMN=∠C=40°,因为旋转前∠AMN=80°,所以旋转角度为40°,故选B.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
在 中,
中, 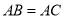 ,点
,点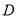 是直线
是直线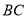 上一点(不与
上一点(不与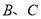 重合),以
重合),以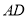 为一边在
为一边在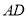 的右侧作
的右侧作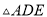 ,使
,使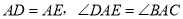 ,连接
,连接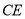 .
.
(1)如图1,当点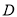 在线段
在线段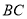 上,如果
上,如果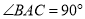 ,则
,则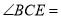 度;
度;
(2)设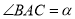 ,
, 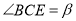 .
.
如图2,当点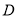 在线段
在线段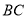 上移动,则
上移动,则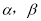 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
如图,将△ABC绕点A旋转到△ADE ,∠BAC=75°,∠DAC=25°,则∠CAE=____°.

查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
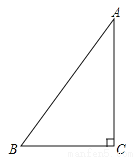
如图,△ABC中,∠C=Rt∠,AB=5cm,BC=3cm,若动点 P从点C开始,按C-A-B-C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t满足什么条件时,△BCP为直角三角形?
(3)另有一点Q,从点C开始,按C-B-A-C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com