
С����С�������������ͬһƷ�ֵĸ��ᣬС����10ԪǮ��������ϸ���ᣬС����10ԪǮ����һ���ָ��ᣬ���˶�˵�Լ���Ļ��㡣��֪��ÿ��ϸ�����ÿ���ָ����ʳ�ò��ֵij�����ͬ��ÿ��ϸ�����ֱ����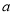 cm,ÿ���ָ����ֱ����1.5
cm,ÿ���ָ����ֱ����1.5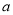 cm,����Ϊ
cm,����Ϊ
A. С������ B ��С������ C������һ������ D��˵����˭����
B ����������Ϊ���˻�����ͬ�����᳤����ȣ����Խ�������� С���� ��С���� �� ��> ����С������. ��ѡ��B. 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017��������Ǹ����п���ѧģ���Ծ� ���ͣ������
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����DE��AC��AE��BD����֤���ı���AODE�Ǿ��Σ�
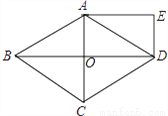
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ���ѡ��
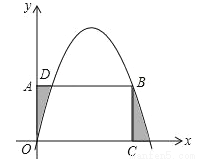
��ͼ��������y=-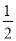 x2+
x2+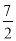 x�����OABC�ı�AB���ڵ�D��B��A��0��3����C��6��0������ͼ�������������OABC�γɵ���Ӱ���ֵ�����ĺ�Ϊ�� ��
x�����OABC�ı�AB���ڵ�D��B��A��0��3����C��6��0������ͼ�������������OABC�γɵ���Ӱ���ֵ�����ĺ�Ϊ�� ��
A��3 B��4 C��5 D��6
A�� �������� �����������DE��OC��E�� ���������ߵĶԳ��Եõ���S��Ӱ=S����OADE�� ��A��0��3���� ��D��������Ϊ3�� ����y=-x2+x�ã�3=-x2+x�� ���x=1��6�� ��AD=1��OA=3�� ��S��Ӱ=S����OADE=1��3=3�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ߺ��н�������2017-2018ѧ�����ѧ�ڰ��꼶�ڶ����¿� ���ͣ������
��ͼ����ABO�ա�CDO����B��CD�ϣ�AO��CD����BOD=30�㣬���A=_______�㣮
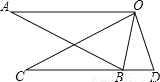
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ߺ��н�������2017-2018ѧ�����ѧ�ڰ��꼶�ڶ����¿� ���ͣ���ѡ��
��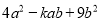 ����ȫƽ��ʽ,����k��ֵΪ�� ��
����ȫƽ��ʽ,����k��ֵΪ�� ��
A. 6 B. 12 C. 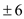 D.
D. 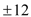
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫ʡ��ݸ�����dz�ѧУ����ѧģ���Ծ� ���ͣ������
��ͼ��AB�ǡ�O��ֱ����C��BD���е㣬CE��AB������ΪE��BD��CE�ڵ�F��

1.��֤��CF=BF��
2.��AD=2����O�İ뾶Ϊ3����BC�ij�
1.����AC����ͼ ��C�ǻ�BD���е� ���BDC=��DBC �֡�BDC=��BAC ��������ABC�У���ACB=90�㣬CE��AB�� ��BCE=��BAC�� ��BCE=��DBC �� CF=BF ��ˣ�CF=BF�� 3�� 2.֤��һ����CG��AD�ڵ�G�� ��C�ǻ�BD���е� ���CAG=��BAC�� ��AC�ǡ�BAD�Ľ�ƽ���ߣ� �� CE=CG��AE...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��㶫ʡ��ݸ�����dz�ѧУ����ѧģ���Ծ� ���ͣ������
���㣺 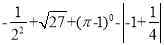
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�괺�˽̰���꼶��ѧ�²ᣨ���������в��� ���ͣ������
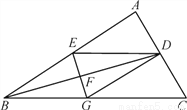
��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������ED��DG.
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC��30�㣬��C��45�㣬ED��4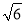 ����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��
����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ຣʡ2017-2018ѧ�����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ������
��ͼ����C��AB�ϣ���M��N�ֱ���AC��BC���е㣬��AC=12cm��BC=10cm�����߶�MN�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com