如图.△ABC中.∠C=90°.tanA=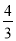.以C为圆心的圆与AB相切于D．若圆C的半径为1.则阴影部分的面积S= ． [解析]连接CD. ∵以C为圆心的圆与AB相切于D.⊙C的半径为1.∠ACB=90°. ∴CD⊥AB.CD=1.S扇形CEF=. ∵tanA=.CD=1. ∴AD=. ∴在Rt△ADC中.由勾股定理可得:AC=. 又∵在Rt△ABC中.tanA= . ∴BC=. ∴S△ 题目和参考答案——青夏教育精英家教网—

如图，△ABC中，∠C=90°，tanA=，以C为圆心的圆与AB相切于D．若圆C的半径为1，则阴影部分的面积S=_____．

【解析】连接CD， ∵以C为圆心的圆与AB相切于D，⊙C的半径为1，∠ACB=90°， ∴CD⊥AB，CD=1，S扇形CEF=， ∵tanA=，CD=1， ∴AD=， ∴在Rt△ADC中，由勾股定理可得：AC=，又∵在Rt△ABC中，tanA= ， ∴BC=， ∴S△ACB=AC•BC=， ∴S阴影=S△ABC﹣S扇形CEF=. 故答案...

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：山东省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

小明用5根木条钉了一个五边形框架，发现它很容易变形，为了使这个框架不变形，他至少要钉________ 根木条加固．

2 【解析】如图所示，加固2根木条即可，故答案为：2．

查看答案和解析>>

科目：初中数学 来源：安徽省2018届九年级上学期第二次月考数学试卷 题型：解答题

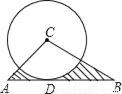
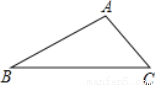
如图，△ABC是一仓库的屋顶的横截面，若∠B=30°，∠C=45°，AC=2，求线段AB的长．

【解析】试题分析：首先过点A作AD⊥BC，根据等腰直角三角形ADC的性质求出CD和AD的长度，根据Rt△ABD的性质求出AB的长度．试题解析：【解析】过点A作AD⊥BC， ∵∠C=45°， ∴∠DAC=45°， ∴AD=CD， ∵AD2+CD2=AC2． ∴AD=，在Rt△ABD中，AB2=AD2+BD2， ∵∠BAD=30°， ∴AB=2AD，解得AB=2． ...

查看答案和解析>>

科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠AOB＝α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．

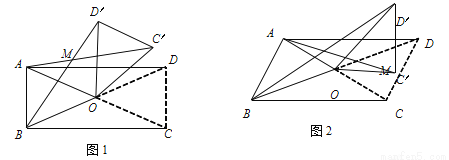
(1)、当四边形ABCD为矩形时，如图1．求证：△AOC′≌△BOD′．

(2)、当四边形ABCD为平行四边形时，设AC＝kBD，如图2．

①猜想此时△AOC′与△BOD′有何关系，证明你的猜想；

②探究AC′与BD′的数量关系以及∠AMB与α的大小关系，并给予证明．

（1）见解析；（2）①、△BOD′∽△AOC′；（2）AC′=kBD′，∠AMB＝α．【解析】试题分析：（1）证明：在矩形ABCD中，AC=BD，OA=OC=AC，OB=OD=BD，∴OA=OC=OB=OD，又∵OD=OD′，OC=OC′，∴OB=OD′=OA=OC′，∵∠D′OD=∠C′OC，∴180°﹣∠D′OD=180°﹣∠C′OC，∴∠BOD′=∠AOC′，∴在△BOD′和△AOC...

查看答案和解析>>

科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：填空题

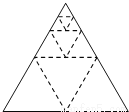
将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表．则an= ．（用含n的代数式表示）

所剪次数	1	2	3	4	…	n
正三角形个数	4	7	10	13	…	an

3n+1．【解析】试题分析：从表格中的数据，不难发现：多剪一次，多3个三角形．即剪n次时，共有4+3（n﹣1）=3n+1．【解析】故剪n次时，共有4+3（n﹣1）=3n+1．

查看答案和解析>>

科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：单选题

不等式1＋x＜0的解集在数轴上表示正确的是（）

A． B． C． D．

A 【解析】试题分析：先解除不等式x﹤-1,在数轴上画出，小于向左画，不包括-1，应画空心圈。

查看答案和解析>>

科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：单选题

下列等式正确的是（　　）

A. 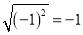B. 22×23=26 C. 20=0 D. （﹣1）﹣2=1

D 【解析】A选项中，因为，所以本选项错误； B选项中，因为，所以本选项错误； C选项中，因为，所以本选项错误； D选项中，因为，所以本选项正确；故选D.

查看答案和解析>>

科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型：填空题

，，若，，则__________．

【解析】由题意得： ∵，． ∴， ∴．

查看答案和解析>>

科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：解答题

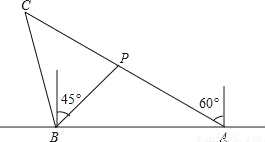
如图，在一笔直的海岸线上有A，B两个观测站，A观测站在B观测站的正东方向，有一艘小船在点P处，从A处测得小船在北偏西60°方向，从B处测得小船在北偏东45°的方向，点P到点B的距离是3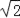千米．（注：结果有根号的保留根号）

（1）求A，B两观测站之间的距离；

（2）小船从点P处沿射线AP的方向以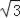千米/时的速度进行沿途考察，航行一段时间后到达点C处，此时，从B测得小船在北偏西15°方向，求小船沿途考察的时间．

（1）(3+3)千米；（2）3小时．【解析】试题分析：（1）过点P作PD⊥AB于点D.先解Rt△PBD，得到BD和PD的长，再解Rt△PAD，得到AD和AP的长，然后根据BD+AD=AB，即可求解；（2）过点B作BF⊥AC于点F.先解Rt△ABF，得出BF和AF的长，再解Rt△BCF，得出CF的长，可求PC=AF+CF-AP，从而求解．试题解析：(1)如图，过点P作PD⊥AB于...

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学