
在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
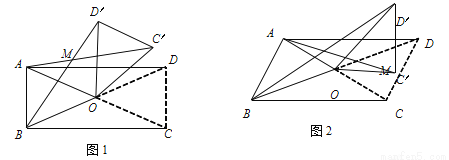
(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
(1)见解析;(2)①、△BOD′∽△AOC′;(2)AC′=kBD′,∠AMB=α. 【解析】试题分析:(1)证明:在矩形ABCD中,AC=BD,OA=OC=AC,OB=OD=BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC...科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B.求证:DF=CE.

查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
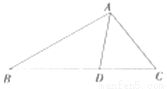
A. 3:2 B. 4:6 C. 9:4 D. 不能确定
A 【解析】试题解析:过点D作DE⊥AB于E,DF⊥AC于F. ∵AD为∠BAC的平分线, ∴DE=DF,又AB:AC=3:2, ∴S△ABD:S△ACD=(AB•DE):(AC•DF)=AB:AC=3:2. 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
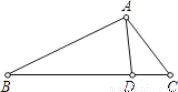
如图,若∠B=∠DAC,则△ABC∽_______,对应边的比例式是___________.
查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:单选题
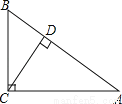
如图,在Rt△ABC中,∠ACB=90,CD⊥AB,垂足为D,若AC=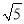 ,BC=2.则sin∠ACD的值为( )
,BC=2.则sin∠ACD的值为( )
A. 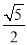 B.
B. 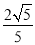 C.
C. 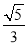 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
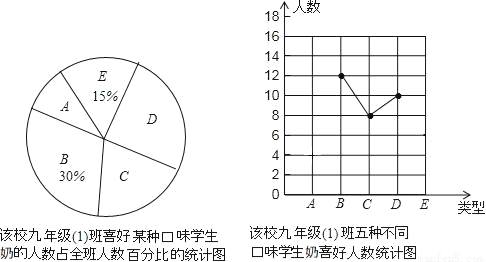
为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.
(1)该班共有多少人?
(2)求出喜好A和E学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
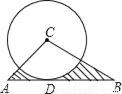
如图,△ABC中,∠C=90°,tanA=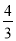 ,以C为圆心的圆与AB相切于D.若圆C的半径为1,则阴影部分的面积S=_____.
,以C为圆心的圆与AB相切于D.若圆C的半径为1,则阴影部分的面积S=_____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
如图,某高楼顶部有一信号发射塔,在矩形建筑物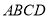 的
的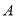 ,
, 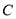 两点处测得该塔顶端
两点处测得该塔顶端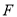 的仰角分别为
的仰角分别为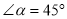 ,
, 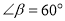 ,矩形建筑物宽度
,矩形建筑物宽度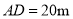 ,高度
,高度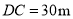 .计算该信号发射塔顶端到地面的高度
.计算该信号发射塔顶端到地面的高度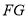 (结果精确到
(结果精确到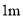 ,
, 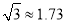 ).
).
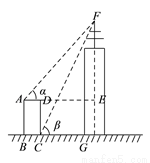
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:单选题
如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( )
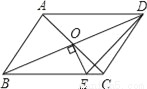
A. 10 B. 16 C. 18 D. 20
D 【解析】∵四边形ABCD是平行四边形, ∴OB=OD,AB=CD,AD=BC, ∵OE⊥BD,∴BE=DE, ∵△CDE的周长为10, 即CD+DE+EC=10, ∴平行四边形ABCD的周长为:AB+BC+CD+AD=2(BC+CD)=2(BE+EC+CD)=2(DE+EC+CD)=2×10=20, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com