
若圆锥的底面圆的半径为2 cm,母线长为8 cm,则这个圆锥侧面展开图的面积为_____cm2.
16π 【解析】圆锥的侧面展开图是扇形,设圆锥底面圆的半径为R,圆锥的母线为l, ∵R=2cm,l=8cm, ∴=πRl=16π(cm²).故答案为:16π. 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
在多项式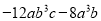 中应提取的公因式是( ).
中应提取的公因式是( ).
A. 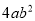 B.
B. 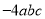 C.
C. 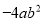 D.
D. 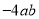
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
如图,AB=AC=4,∠A=45°,P为BC边上的一个动点,PD⊥AB于点 D,PE⊥AC于点E,则PE+PD=______.
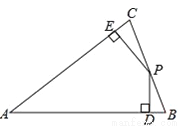
查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:解答题
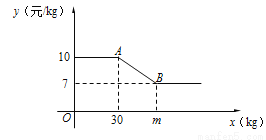
某水果店经营某种水果,顾客的批发量x(kg)与批发单价y(元/kg)之间的关系如图所示.图中线段AB表示:批发量x每增加1 kg,批发单价y降低0.1元/kg.
(1)求m的值;
(2)已知该水果进价为6元/kg,设该水果店获利w元.
①求w与x的函数表达式;
②当0<x≤m时,求w的最大值.
查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:解答题
一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,求摸到蓝球的概率;
(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.
求至少有1次摸到红球的概率.
(1);(2). 【解析】分析:(1)列举出所有的可能结果,找到恰是蓝球的结果,根据概率公式计算即可, (2)列举出所有可能出现的结果,找到至少有一次是红球的结果,根据概率公式计算即可. 本题解析: (1)搅匀后从中任意摸出1个球,所有可能出现的结果有:红、红、蓝、共有3种,它们出现的可能性相同.所有的结果中,满足“恰好是蓝球”(记为事件A)的结果只有1种,所以;. ...查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:填空题
把二次函数y=x2的图像沿x轴向左平移3个单位长度,再沿y轴向上平移1个单位长度后,所得图像的函数表达式为_________.
y=(x+3)2+1(或y=x2+6x+10) 【解析】二次函数y=x²的顶点坐标为(0,0),把点(0,0)沿x轴向左平移3个单位,再沿y轴向上平移1个单位所得对应点的坐标为(?3,1),所以平移后的抛物线解析式为y=(x+3)2=1. 故答案为y=(x+3)²+1(或y=x2+6x+10).查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:单选题
在比例尺为1∶500000的工程图上,南京地铁四号线全长约6.76 cm,它的实际长度约为( )
A. 3.38 km B. 338 km C. 33.8 km D. 0.338 km
C 【解析】解:设地铁线的实际长度约为xcm. 根据比例尺的定义:比例尺=图上距离:实地距离,可得 解之得 x=33800000 ∵ 33800000cm=33.8km ∴ 它的实际长度为33.8km 故选C.查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:填空题
如图,AB∥CD,S△ABE:S△CDE=1:4,则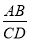 =___________
=___________
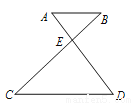
查看答案和解析>>
科目:初中数学 来源:北京市东城区2017-2018学年度第一学期期末教学目标检测初二数学试卷 题型:解答题
如图,点E,F在线段AB上,且AD=BC,∠A=∠B,AE=BF.求证:DF=CE.
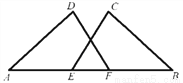
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com