
如图,AB∥CD,S△ABE:S△CDE=1:4,则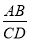 =___________
=___________
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:单选题
把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A. 16 B. 17 C. 18 D. 19
A 【解析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n-1)边形.故当剪去一个角后,剩下的部分是一个18边形,则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形. 故选:A.查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:填空题
若圆锥的底面圆的半径为2 cm,母线长为8 cm,则这个圆锥侧面展开图的面积为_____cm2.
16π 【解析】圆锥的侧面展开图是扇形,设圆锥底面圆的半径为R,圆锥的母线为l, ∵R=2cm,l=8cm, ∴=πRl=16π(cm²).故答案为:16π.查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:解答题
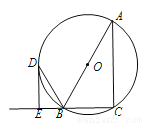
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE∥AC交CB的延长线于E.
(1)求证:DE是⊙O的切线;
(2)若∠A=30°,求证:BD=BC.
查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:解答题
解方程:x2+4x=1.
, . 【解析】分析:方程两边加上4得到(x+2)²=5,然后利用直接开平方法解方程. 本题解析: 解: ∴ ∴查看答案和解析>>
科目:初中数学 来源:南京市溧水区2016~2017学年度第一学期期末九年级试卷 题型:填空题
把二次函数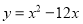 化为形如
化为形如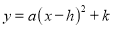 的形式:____________
的形式:____________
查看答案和解析>>
科目:初中数学 来源:广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
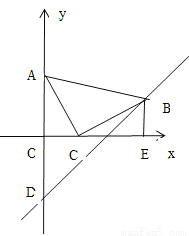
在平面直角坐标系中,将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,∠ACB=900,且A(0,4),点C(2,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D。
(1)求证;△AOC≌△CEB
(2)求△ABD的面积。
查看答案和解析>>
科目:初中数学 来源:广东省揭阳市揭西县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
一次函数y=2x-3与y轴的交点坐标为( )
A. (0,-3) B. (0,3) C. (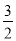 ,0) D. (
,0) D. (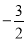 ,0)
,0)
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型:解答题
先化简,再求值: 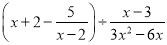 ,其中
,其中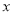 满足
满足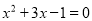 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com