
某厂前年缴税30万元,今年缴税36.3万元,若该厂缴税的年平均增长率为x,则可列方程( )
A. 30x2=36.3 B. 30(1-x)2=36.3
C. 30+30(1+x)+30(1+x)2=36.3 D. 30(1+x)2=36.3
D 【解析】如果设该厂缴税的年平均增长率为x, 那么根据题意得今年缴税30(1+x)2 , 列出方程为:30(1+x)2=36.3, 故选D. 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型:单选题
一元二次方程x2-x-2 = 0的解是( )
A. x1=1,x2=2 B. x1=1,x2=﹣2 C. x1=﹣1,x2=﹣2 D. x1=﹣1,x2=2
D 【解析】由题意x2-x-2=0, 分解因式得(x-2)(x+1)=0, 所以x-2=0,或x+1=0 即x=2或x=-1 选D.查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:单选题
独山县开展关于精准扶贫、精准扶贫的决策部署以来,某贫困户2014年人均纯收入为2620元,经过帮扶到2016年人均纯收入为3850元,设该贫困户每年纯收入的平均增长率为x,则下面列出的方程中正确的是( )
A. 2620(1+x)2=3850 B. 2620(1+x)=3850
C. 2620(1+2x)=3850 D. 2620(1+x)2=3850
A 【解析】由题意得2620(1+x)2=3850.故选A.查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:填空题
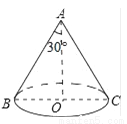
如图,已知圆锥的高为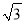 ,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:单选题
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则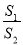 =
=
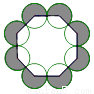
A. 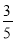 B.
B. 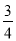 C.
C. 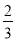 D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:解答题
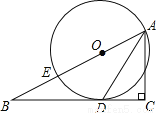
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:填空题
如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米,该抛物线的函数表达式为 ______ .
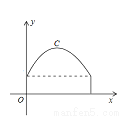
查看答案和解析>>
科目:初中数学 来源:湖北省元月联合测试数学试卷 题型:解答题
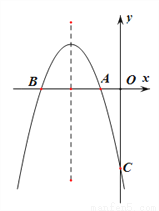
如图,已知抛物线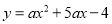 交
交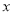 轴于点
轴于点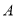 、点
、点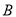 ,交
,交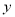 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求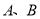 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点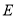 异于
异于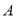 ,且
,且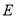 在对称轴右侧),直线
在对称轴右侧),直线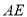 交对称轴于N,
交对称轴于N,
直线BE交对称轴于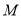 ,对称轴交
,对称轴交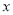 轴于
轴于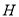 ,试确定
,试确定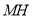 、
、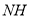 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:单选题
已知甲车行驶30千米与乙车行驶40千米所用时间相同,并且乙车每小时比甲车多行驶15千米.若设甲车的速度为x千米/时,依题意列方程正确的是( )
A.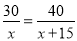 B.
B.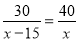
C.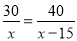 D.
D.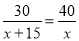
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com