练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个两位数，个位数字是十位数字的4倍，如果把个位数字与十位数字对调，那么得到的新数比原数大54，则原数为________．

    28 【解析】【解析】 设原数十位数字为x，则个位数字为4x，根据题意可得： 40x+x﹣（10x+4x）=54，解得：x=2，故4x=8． 故原数为28．故答案为：28．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：填空题

    不等式组的非负整数解有__________个。

    6 【解析】 由①得：x>?1， 由②得：x≤5， 不等式组的解集为：?1

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：解答题

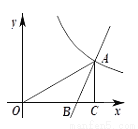
    如图，直线y1＝2x－3与双曲线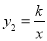在第一象限交于点A，与x轴交于点B，过点A作AC⊥x轴，垂足为C，已知∠BAC＝∠AOC．

    （1）求A，B两点的坐标及k的值；

    （2）请直接写出当y2＞y1＞0时x的取值范围．

    （1）k=2；（2）＜x＜2 【解析】试题分析：（1）根据直线与x轴的交点，令y=0，求出点B的坐标，然后根据解直角三角形求出A点的坐标，利用待定系数法求出k的值； （2）根据函数的图像和交点，直接可写出取值范围. 试题解析：由y1＝2x－3=0，解得，所以B(，0)，OB=. 设点A的横坐标为m(m>0)，则纵坐标为2m-3,BC= ，AC=2m-3， ∵AC⊥x轴...

    查看答案和解析>>

    科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：单选题

    过⊙O内一点M的最长弦长为10cm，最短弦长为8cm，那么OM长为（ ）

    A. 3cm B. 6cm C. 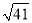cm D. 9cm

    A 【解析】试题分析：由题意知，最长的弦为直径，最短的弦为垂直于直径的弦，如图所示． 直径ED⊥AB于点M， 则ED=10cm，AB=8cm， 由垂径定理知：点M为AB中点， ∴AM=4cm， ∵半径OA=5cm， ∴OM2=OA2-AM2=25-16=9， ∴OM=3cm． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：解答题

    根据以下对话，分别求小红所买的笔和笔记本的价格．

    3.6元 【解析】试题分析：根据图中小红的回答，若设笔的价格为x元/支，则笔记本的价格为3x元/本．根据10支笔和5本笔记本花了30元钱，列出一元一次方程组10x+5×3x=30，解得x值，那么小红所买的笔和笔记本的价格即可确定． 试题解析：【解析】 设笔的价格为x元/支，则笔记本的价格为3x元/本 由题意，10x+5×3x=30 解之得x=1.2，3x=3.6 答...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：单选题

    一元一次方程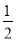x－1＝2的解表示在数轴上，是图中数轴上的哪个点(　　)

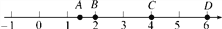
    A. D点 B. C点 C. B点 D. A点

    A 【解析】【解析】 方程去分母得：x﹣2=4，解得：x=6，把方程的解表示在数轴上，是图中数轴上的D点，故选A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：单选题

    小马虎在做作业，不小心将方程中的一个常数污染了，被污染的方程是2（x－3）－■＝x＋1，怎么办呢？他想了想便翻看书后的答案，方程的解是x＝9，请问这个被污染的常数是（　　）

    A. 1 B. 2 C. 3 D. 4

    B 【解析】【解析】 设被污染的数字为y． 将x=9代入得：2×6﹣y=10． 解得：y=2． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：单选题

    如图，正五边形ABCDE内接于⊙O，过点A的切线与CB的延长线相交于点F，则∠F=（ ）

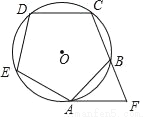
    A. 18° B. 36° C. 54° D. 72°

    D 【解析】试题分析：连接OA、OB， ∵AF是⊙O的切线， ∴∠OAF＝90°， ∵正五边形ABCDE内接于⊙O， ∴∠AOB＝＝72°， ∵OA＝OB， ∴∠OAB＝∠OBA＝＝54°， ∴∠BAF＝90°－54°＝36°， ∵∠ABF＝＝72°， ∴∠F＝180°－36°－72°＝72°， 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：解答题

    如图，∠AOC为直角，OC是∠BOD的平分线，且∠AOB＝35°，求∠AOD的度数．

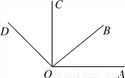
    145° 【解析】试题分析：首先根据∠AOB的度数和∠AOC的度数求出∠BOC的度数，根据角平分线的性质得出∠COD的度数，最后根据∠AOD=∠AOC+∠COD求出答案． 试题解析：【解析】 ∵∠AOC为直角，∴∠AOC＝90°， ∴∠BOC＝∠AOC－∠AOB＝90°－35°＝55°， 又OC平分∠BOD，∴∠COD＝∠BOC＝55°，∴∠AOD＝∠AOC＋∠COD＝9...

    查看答案和解析>>

    同步练习册答案