练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

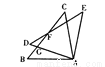
    如图，△ABC≌△ADE，∠DAC=60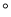，∠BAE=100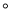,BC、DE相交于点F,则∠DFB度数是( )

    A. 15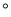 B. 20 C. 25 D. 30

    B 【解析】∵△ABC≌△ADE， ∴∠B=∠D，∠BAC=∠DAE， 又∠BAD=∠BAC-∠CAD，∠CAE=∠DAE-∠CAD， ∴∠BAD=∠CAE， ∵∠DAC=60°，∠BAE=100°， ∴∠BAD=（∠BAE-∠DAC）=×（100°-60°）=20°， 在△ABG和△FDG中，∵∠B=∠D，∠AGB=∠FGD， ∴∠DFB=∠BAD...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：重庆市江北区2018届九年级上期末模拟数学试卷 题型：单选题

    下列图形中，既是轴对称图形又是中心对称图形的是(    )

    A. B. C. D.

    D 【解析】分析：本题考查轴对称图形和中心对成图形的定义. 解析：A选项是轴对称图形不是中心对成图形，故错误；B选项是中心对成图形不是轴对称图形，故错误；C选项是轴对称图形不是中心对成图形，故错误；D选项是轴对称图形和中心对成图形，故正确. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型：填空题

    如图，AB∥CD，直线EF分别交AB、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于_____度．

    30 【解析】试题解析： , 故答案为：30.

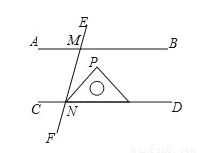
    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：解答题

    先化简，再求值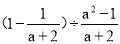： ，其中a=3．

    【解析】试题分析：括号内先通分进行分式加减运算，然后再进行分式除法运算，最后代入数值即可. 试题解析： ， 当a=3时，原式= .

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：填空题

    一个n边形的内角和是900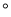，那么n=_____.

    7 【解析】根据多边形内角和公式则有：（n-2）180°=900°， 解得n=7， 故答案为：7．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：单选题

    若分式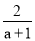有意义，则a的取值范围是( )

    A. a=0 B. a=l C. a≠-l D. a≠0

    C 【解析】由题意得：a+1≠0，解得：a≠1， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：解答题

    省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：

    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    甲

    10

    8

    9

    8

    10

    9

    乙

    10

    7

    10

    10

    9

    8

    （1）根据表格中的数据，计算出甲的平均成绩是 环，乙的平均成绩是 环；

    （2）分别计算甲、乙六次测试成绩的方差；

    （3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．

    计算方差的公式：s2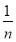＝ [(x1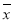－)2＋(x2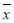－)2＋＋(xn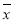－)2]

    （1）9，9；（2），；（3）甲，理由见解析. 【解析】 试题分析：（1）平均数是指在一组数据中所有数据之和再除以数据的个数，所以甲的平均成绩＝（10＋8＋9＋8＋10＋8）÷6＝9，乙的平均成绩＝（10＋7＋10＋10＋9＋8）÷6＝9；（2）应用方差公式，直接计算即可；（3）方差就是和中心偏离的程度，用来衡量一批数据的波动大小在样本容量相同的情况下，方差越大，说明数据的波动越大，越...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：单选题

    对于一元二次方程ax2+bx+c=0 （a≠0），下列说法中错误的是（　　）

    A. 当a＞0，c＜0时，方程一定有实数根

    B. 当c=0时，方程至少有一个根为0

    C. 当a＞0，b=0，c＜0时，方程的两根一定互为相反数

    D. 当abc＜0时，方程的两个根同号，当abc＞0时，方程的两个根异号

    D 【解析】解：A．正确．当a＞0，c＜0时，△=b2﹣4ac＞0，则方程一定有实数根； B．正确．当c=0时，则ax2+bx=0，则方程至少有一个根为0； C．正确．当a＞0，b=0，c＜0时，方程两根为x1，x2，x1+x2==0，则方程的两根一定互为相反数； D．错误．当ac＜0时，方程的两个根异号，当ac＞0时，方程的两个根同号． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：解答题

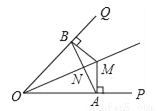
    如图，OM平分∠POQ，MA⊥OP，MB⊥OQ，A、B为垂足，AB交OM于点N．求证：∠OAB=∠OBA．

    证明见解析． 【解析】试题分析:先根据角平分线的性质可证得:MA=MB, 再根据HL定理判定Rt△MAO≌Rt△MBO,然后可证得:OA=OB, 根据等边对等角可证得: ∠OAB＝∠OBA. 试题解析:∵OM平分∠POQ,MA⊥OP,MB⊥OQ, ∴AM=BM, 在Rt△MAO和Rt△MAO中, , ∴Rt△AOM≌Rt△BOM(HL), ∴OA=O...

    查看答案和解析>>

    同步练习册答案