练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一次函数y=（m—1）x+m2的图象过点（0，4），且y随x的增大而增大，则m的值为（ ）

    A. -2 B. 2 C. 1 D. -2或2

    B 【解析】试题分析：把（0，4）代入解析式得， ，解得m=，因为y随x的增大而增大，所以m-1＞0，所以m=-2舍去，只取m=2． 故选：B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：解答题

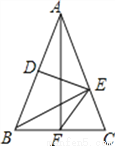
    如图，在△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，

    （1）求证：BF=EF；（2）求∠EFC的度数.

    （1）证明见解析；（2）45°. 【解析】试题分析：（1）由AB=AC，AF⊥BC，可知BF=CF，再由BE⊥AC 根据直角三角形斜边中线等于斜边一半可得BF=EF，从而得到BF=EF； （2）先根据线段垂直平分线的性质及BE⊥AC得出△ABE是等腰直角三角形，再由等腰三角形的性质得出∠ABC的度数，由BF=EF，再根据三角形外角的性质即可得出结论． 试题解析：（1）∵AB=AC...

    查看答案和解析>>

    科目：初中数学 来源：吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型：单选题

    已知正方形①、②在直线上，正方形③如图放置，若正方形①、②的面积分别为81 cm2和144 cm2，则正方形③的边长为（　　）

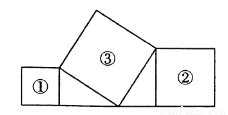
    A. 225 cm B. 63 cm C. 50 cm D. 15 cm

    D 【解析】试题解析：∵四边形①、②、③都是正方形， ∴∠EAB=∠EBD=∠BCD=90°，BE=BD， ∴∠AEB+∠ABE=90°，∠ABE+∠DBC=90°， ∴∠AEB=∠CBD． 在△ABE和△CDB中， ， ∴△ABE≌△CDB（AAS）， ∴AE=BC，AB=CD． ∵正方形①、②的面积分别81cm2和144cm2， ∴AE2=81，CD2=144． ∴A...

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市2018届九年级1月月考数学试卷 题型：填空题

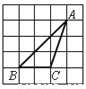
    如图，△ABC的顶点是正方形网格的格点，则sinA的值为__________.

    【解析】试题分析：连接CE，根据图形可知AC=，BE=CE=，∠EBC=∠ECB=45°，∴CE⊥AB，∴sinA==． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：山东省济南市2018届九年级1月月考数学试卷 题型：单选题

    抛物线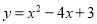的图象向右平移2个单位长度后所得新的抛物线的顶点坐标为（ ）

    A. （4，-1） B. （0，-3） C. （-2，-3） D. （-2，-1）

    A 【解析】【解析】 ∵抛物线y=x2﹣4x+3可化为：y=（x﹣2）2﹣1，∴其顶点坐标为（2，﹣1），∴向右平移2个单位得到新抛物线的解析式，所得抛物线的顶点坐标是（4，﹣1）．故选A．

    查看答案和解析>>

    科目：初中数学 来源：福建省汀东教研片六校2018届九年级10月月考数学试卷 题型：解答题

    随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加.据统计，某小区2015年底拥有家庭轿车64辆，2017年底家庭轿车的拥有量达到100辆.

    （1）若该小区2015年底到2018年底家庭轿车拥有量的年平均增长率都相同，求该小区到2018年底家庭轿车将达到多少辆？

    （2）为了缓解停车矛盾，该小区决定投资15万元再建造若干个停车位.据测算，建造费用分别为室内车位5000元/个，露天车位1000元/个，考虑到实际因素，计划露天车位的数量不少于室内车位的2倍，但不超过室内车位的2.5倍，求该小区最多可建两种车位各多少个？试写出所有可能的方案.

    方案一：建室内车位20个，露天车位50个；方案二：室内车位21个，露天车位45个. 【解析】试题分析：（1）设家庭轿车拥有量的年平均增长率为x，根据2015年底拥有家庭轿车64辆，2017年底家庭轿车的拥有量达到100辆列出方程，求出平均增长率，即可计算出2018年家庭轿车的数量； （2）设该小区可建室内车位a个，露天车位b个，根据总投资是15万元建立a、b的关系，然后用a去表示b，根...

    查看答案和解析>>

    科目：初中数学 来源：福建省汀东教研片六校2018届九年级10月月考数学试卷 题型：解答题

    如图，二次函数y=（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．

    （1）求二次函数与一次函数的解析式；

    （2）根据图象，写出满足kx+b≥（x-2）2+m的x的取值范围．

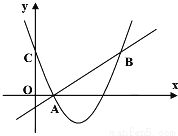
    （1）y=（x-2）2-1 y=x-1 （2）1≤x≤4 【解析】（1）先将点A（1，0）代入y=（x﹣2）2+m求出m的值，根据点的对称性确定B点坐标，然后根据待定系数法求出一次函数解析式； （2）根据图象和A、B的交点坐标可直接求出kx+b≥（x﹣2）2+m的x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：福建省汀东教研片六校2018届九年级10月月考数学试卷 题型：单选题

    下列方程中，你最喜欢的一个一元二次方程是（ ）

    A. 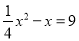B. x3-x2+40=0 C. 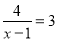D. 3x3-2xy+y2=0

    A 【解析】试题分析：A、是一元二次方程，故此选项正确； B、是一元三次方程，故此选项错误； C、是分式方程，故此选项错误； D、二元三次方程，故此选项错误． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上学期第二次月考数学试卷 题型：单选题

    下列四个生产生活现象，可以用基本事实“两点之间线段最短”来解释的是（ ）

    A. 用两个钉子就可以把木条固定在墙上

    B. 植树时，只要定出两棵树的位置，就能确定同一行树所在的直线

    C. 从A地到B地架设电线，总是尽可能沿着线段AB来架设

    D. 打靶的时候，眼睛要与枪上的准星、靶心在同一条直线上

    C 【解析】解：A、属于使得物体比较稳定，故本选项不符； B、属于两点确定一条直线，故本选项不符； C、这是正确的，两点之间线段最短，减少了距离，故本选项正确； D、属于两点确定一条直线，故本选项不符； 故选C．

    查看答案和解析>>

    同步练习册答案