
 用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.
用两个全等的等边△ABD和△BCD拼成如图的菱形ABCD.现把一个含60°角的三角板与这个菱形叠合,使三角板的60°角的顶点与点D重合,两边分别与DA、DB重合.将三角板绕点D逆时针方向旋转.
|
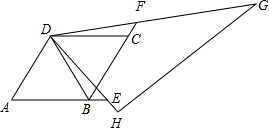 (2)∵△ABD和△BCD是等边三角形,
(2)∵△ABD和△BCD是等边三角形,
|


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
| 22 |
| 7 |
| 3 | 27 |
| •• |
| 17 |
| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P.
如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N,交BE于P.| MF |
| FN |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)
小霞和爸爸、妈妈到人民公园游玩,回家后,她利用平面直角坐标系画出了公园的景区地图,(横轴和纵轴均为小正方形的边所在直线,每个小正方形边长为1个单位长度)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com