练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将三角尺的直角顶点放在直线a上，a∥b，∠1=50°，∠2=60°，则∠3的度数为（ ）

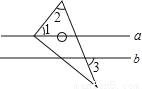
    A．50° B．60° C．70° D．80°

    C. 【解析】 试题解析：∵△BCD中，∠1=50°，∠2=60°， ∴∠4=180°-∠1-∠2=180°-50°-60°=70°， ∴∠5=∠4=70°， ∵a∥b， ∴∠3=∠5=70°． 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第21章 一元二次方程 单元测试卷 题型：填空题

    已知关于x的一元二次方程x2﹣2x+k=0有两个相等的实数根，则k值为 ．

    3 【解析】试题解析：根据题意得△=（-2）2-4k=0， 解得k=3．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 同步测试 1.3 同底数幂的除法 题型：单选题

    （）0是（　　）

    A. B. 1 C. D. ﹣1

    B 【解析】任何一个不等于零的数的零次幂都等于1，由此可得（）0=1，故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型：解答题

    如图,已知DE∥BC,且BE,DF分别平分∠ABC,∠ADE,则DF∥BE.请说明理由.

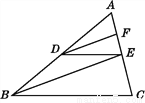
    证明见解析 【解析】试题分析：根据平行线的性质与判定，结合角平分线的定义作答即可． 试题解析：证明：∵DE∥BC，∴∠ADE=∠ABC（两直线平行，同位角相等）． 又∵DF、BE分别平分∠ADE和∠ABC，∴∠ADF=∠ADE，∠ABE=∠ABC， ∴∠ADF=∠DBE，∴DF∥BE（同位角相等，两直线平行）．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.3.1 平行线的性质 同步练习 题型：单选题

    如图，已知a∥b,直角三角板的直角顶点在直线b上，若∠1=60°，则下列结论错误的是（ ）

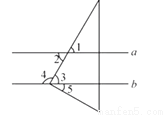
    A．∠2=60° B．∠3=60° C．∠4=120° D．∠5=40°

    D 【解析】 试题分析：根据平行线的性质和对顶角的性质得出∠3=∠2=∠1=60°，根据互补的性质可得：∠4=180°-60°=120°，根据互补的性质可得：∠5=90°-60°=30°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型：解答题

    世界上最大的金字塔是埃及的胡夫金字塔，这座金字塔共用了约为2.3×106块巨石，每块巨石的质量约为2.5×103kg，胡夫金塔所用巨石的总质量约为多少千克？

    5.75×109(kg) 【解析】试题分析：根据同底数幂的乘法进行法则进行计算，将最后的结果写成科学计数法的形式即可得出答案． 试题解析： (千克) 答：胡夫金塔所用巨石的总质量约为千克．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型：填空题

    计算下列各题：

    (1)2xy2·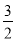xy＝______；

    (2)(－2a2b3)·(－3a)＝_____；

    (3)(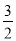－m2n)·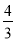mn2q＝_______；

    (4)(4×105)·(5×107)＝_______.

    3x2y3 6a3b3 －2m3n3q 2×1013 【解析】试题分析：同底数幂的乘法法则：底数不变，指数相加．首先将系数进行相乘，然后根据同底数幂的乘法计算法则得出答案．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 单项式与多项式相乘 专题练习题 含答案 题型：单选题

    一个长方体的长、宽、高分别是3x－4,2x和x，则它的体积等于( )

    A. 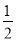(3x－4)·2x＝3x3－4x3 B. 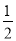x·2x＝x2

    C. (3x－4)·2x·x＝6x3－8x2 D. 2x(3x－4)＝6x2－8x

    C 【解析】试题分析：长方体的体积=长×宽×高，则，故选C．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市张家港市2016-2017学年九年级（上）期末数学试卷 题型：解答题

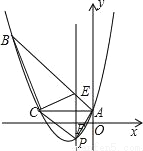
    如图，已知抛物线y=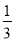x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．

    （1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

    （3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

    （1）y= x2+2x+1（2）P（﹣，﹣）（3）Q（﹣4，1）或（3，1） 【解析】试题分析：（1）用待定系数法求出抛物线解析式即可； （2）设点P（m， m2+2m+1），表示出PE=﹣m2﹣3m，再用S四边形AECP=S△AEC+S△APC=AC×PE，建立函数关系式，求出极值即可； （3）先判断出PF=CF，再得到∠PCF=∠EAF，以C、P、Q为顶点的三角形与△ABC相...

    查看答案和解析>>

    同步练习册答案