
多边形的每个内角都等于150°,则这个多边形的边数为___,对角线条数为__.
12 54 【解析】【解析】 ∵多边形的每个内角都等于150°,∴多边形的每个外角都=180°-150°=30°,∴边数n=360°÷30°=12.对角线条数=12×(12-3)÷2=54.故答案为:12,54.科目:初中数学 来源:陕西省2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
已知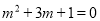 ,则
,则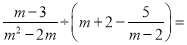 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型:填空题
在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是 .
(0,﹣3). 【解析】 试题分析:∵点(﹣2,3)关于原点的对称点为:(2,﹣3), ∴(2,﹣3)再向左平移2个单位长度得到的点的坐标是:(0,﹣3). 故答案为:(0,﹣3).查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:填空题
从十二边形的一个顶点出发可引_________条对角线,把十二边形分成_______个三角形.
A. 9 10 B. 10 11 C. 11 12 D. 12 13
A 【解析】【解析】 从十二边形的一个顶点出发可引对角线条数:12-3=9,把十二边形分成的三角形个数:9+1=10.故选A.查看答案和解析>>
科目:初中数学 来源:天津武清区数学试卷八年级《11.3 多边形及其内角和》同步测试 题型:单选题
若四边形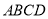 中,∠A:∠B:∠C:∠D=1:2:4:5,则
中,∠A:∠B:∠C:∠D=1:2:4:5,则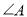 与
与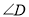 的度数分别是( )
的度数分别是( )
A. 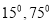 ; B.
; B. 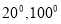 ; C.
; C. 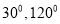 ; D.
; D.  .
.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
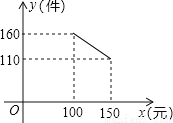
为发展“低碳经济”,某单位花12500引进了一条环保型生产线生产新产品,在生产过程中,每件产品还需成本40元,物价部门规定该产品售价不得低于100元/件且不得高于150元/件,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一个月该单位是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一个月盈利最大或亏损最小时,第二个月公司重新确定产品售价,能否使两个月共盈利达10800元?若能,求出第二个月的产品售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:解答题
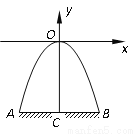
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:解答题
解方程:(1)2y2+5y=7.(公式法) (2)y2-4y+3=0(配方法)
(1)y=1或y=;(2)y=3或y=1. 【解析】试题分析:(1)整理成一般式,利用求根公式求解可得; (2)移项后,两边都加上4配成完全平方式,再开方求解可得. 【解析】 (1)原方程整理成一般式可得2y2+5y-7=0, ∵a=2,b=5,c=-7, ∴△=25-4×2×(-7)=81>0, 则y=, ∴y=1或y=; (2)∵y2-4y=-...查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:单选题
某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A. 22+x=2×26
B. 22+x=2(26-x)
C. 2(22+x)=26-x
D. 22=2(26-x)
B 【解析】设第二组调到第一组x人,则第一组的现有人数为:(22+x)人,第二组的现有人数为:(26-x)人,又由于第一组现有人数是第二组的2倍,因此可列方程为: 22+x=2(26-x),故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com