
��ͼ����֪�����ߣ�����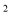 ���������
���������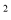 ��4�ᣭ4������ཻ�ڵ�A�͵�B��������ཻ�ڵ�D��0��8����ֱ��DCƽ���ڣ��ᣬ������������һ��C������P��ÿ��2����λ���ȵ��ٶȴ�C���������C��D�˶���ͬʱ����Q��ÿ��1����λ���ȵ��ٶȴӵ�A��������A��B�˶�������PQ��CB�����P�˶���ʱ��Ϊt�룮
��4�ᣭ4������ཻ�ڵ�A�͵�B��������ཻ�ڵ�D��0��8����ֱ��DCƽ���ڣ��ᣬ������������һ��C������P��ÿ��2����λ���ȵ��ٶȴ�C���������C��D�˶���ͬʱ����Q��ÿ��1����λ���ȵ��ٶȴӵ�A��������A��B�˶�������PQ��CB�����P�˶���ʱ��Ϊt�룮
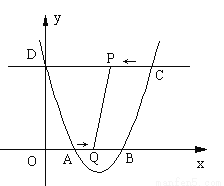
����������ֵ�����������ı���ODPQΪ����ʱ����������ε���������������ı���PQBC���������14ʱ����t��ֵ����������tΪ��ֵʱ����PBQ�ǵ��������Σ���ֱ��д���𰸣�
������8������������������ ���������������� �������������ߣ�������������ᣭ4�ᣭ4�����㣨0��8�� ��ᣭ4�ᣭ4��8 ��ã��6�����2���������⣬��ȥ�� ����ֵΪ6 �������ɣ������ɵ������ߵĽ���ʽΪ ��������6����8 ������0ʱ������6����8��0 ��ã�����2������4 ��A������Ϊ��2��0����B������Ϊ��4��0�� ������... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���ຣʡ2017-2018ѧ�����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ������
���� 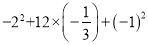
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���(x��1)2��2016��0�ĸ��������( )
A. ��������ȵ�ʵ���� B. ����������ȵ�ʵ����
C. ֻ��һ��ʵ���� D. ��ʵ����
D ��������һԪ���η���(x+1)2+2016=0��Ϊx2+2x+2017=0�� �ߡ�=4?4��1��2017<0�� ��ԭ������ʵ����. ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ������
���һ������������ǵ�һ�룬��ô�������_______
30�� �����������������������ǵĶ���Ϊx�㣬��������ɵã�x=����ã�x=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��̨�е�����������2017-2018ѧ��ȵ�һѧ�ڵ����νμ�����꼶��ѧ�Ծ� ���ͣ���ѡ��
С���Ĵ��xԪ��С�ֵĴ���С����һ�뻹��2Ԫ��С�ֵĴ���ǣ�������
A. 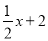 B.
B. 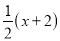 �� C.
�� C. 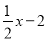 D.
D. 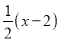
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
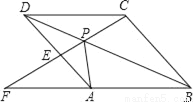
��ͼ����P������ABCD�ĶԽ���BD��һ�㣬����CP���ӳ�����AD��E����BA���ӳ����ڵ�F��
���ʣ���1��ͼ�С�APD���ĸ�������ȫ�ȣ���˵�����ɣ�
��2����֤��PA2=PE•PF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
�ֽ���ʽ��x2+4+4x��y2=_____��
��x+y+2����x��y+2�� �����������������ԭʽ �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ �������� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���֪������C1��y=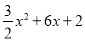 �Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮
�Ķ���ΪM����y���ཻ�ڵ�N���Ƚ�������C1��x�ᷭ�ۣ�������ƽ��p����λ���Ⱥ�õ�������C2��ֱ��l��y=kx+b����M��N���㣮
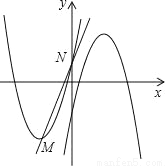
��1�����ͼ��ֱ��д������ʽ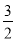 x2+6x+2��kx+b�Ľ⼯��
x2+6x+2��kx+b�Ľ⼯��
��2����������C2�Ķ������M����ԭ��Գƣ���p��ֵ��������C2�Ľ���ʽ��
��3����ֱ��l��y������ƽ��q����λ���Ⱥ��루2���е�������C2���ڹ����㣬
��3��4q�����ֵ��
���𰸡���1����2��x��0��2��y=��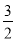 x2+6x��2��3����q=
x2+6x��2��3����q= ʱ��3��4qȡ���ֵ�����ֵΪ��7
ʱ��3��4qȡ���ֵ�����ֵΪ��7
�����������������(1)�����ȸ��ݶ��κ����Ľ���ʽ�ֱ������M�͵�N�����꣬Ȼ�����ͼ��ó�����ʽ��ȡֵ��Χ��(2)�����ݷ��۵ó������ߵĶ�������Ϳ��ڷ����Լ���С���Ӷ��ó������ߵĺ�������ʽ��(3)�����Ƚ���M�͵�N���������һ�κ�������ʽ�ó�һ�κ����Ľ���ʽ��Ȼ����ƽ�ƺ�Ľ���ʽΪy=3x+2-q��Ȼ��������������н���ó�������ʵ�������Ӷ��ó����ֵ.
�����������1����y=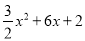 ��x=0����y=2��
��x=0����y=2��
��N��0��2���� ��y=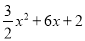 =
=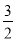 ��x+2��2��4�� ��M����2����4����
��x+2��2��4�� ��M����2����4����
�۲캯��ͼ���֣�����2��x��0ʱ��������C1��ֱ��l���·���
���ʽ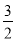 x2+6x+2��kx+b�Ľ⼯Ϊ��2��x��0��
x2+6x+2��kx+b�Ľ⼯Ϊ��2��x��0��
��2����������C1��y=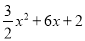 �Ķ���ΪM����2����4����
�Ķ���ΪM����2����4����
��x�ᷭ�ۺ�ĶԳƵ�����Ϊ����2��4���� ��������C2�Ķ������M����ԭ��Գƣ�
��������C2�Ķ�������Ϊ��2��4���� ��p=2������2��=4��
��������C2��C1���ڴ�С��ͬ�����ڷ����෴��
��������C2�Ľ���ʽΪy=��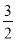 ��x��2��2+4=��
��x��2��2+4=��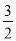 x2+6x��2��
x2+6x��2��
��3����M����2����4����N��0��2������y=kx+b�У��ã� 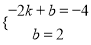 ����ã�
����ã� 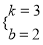 ��
��
��ֱ��l�Ľ���ʽΪy=3x+2��
����ֱ��l��y������ƽ��q����λ���Ⱥ���������C2���ڹ����㣬
��̩�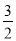 x2+6x��2=3x+2��q��ʵ��������3x2��6x+8��2q��ʵ������
x2+6x��2=3x+2��q��ʵ��������3x2��6x+8��2q��ʵ������
���=����6��2��4��3����8��2q����0����ã�q��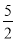 �� �ߩ�4��0��
�� �ߩ�4��0��
�൱q=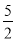 ʱ��3��4qȡ���ֵ�����ֵΪ��7��
ʱ��3��4qȡ���ֵ�����ֵΪ��7��
�㾦��������Ҫ����ľ��Ƕ��κ�����ͼ�������ʡ�һ�κ��������ʡ����κ�����һ�κ����Ĵ�С�Ƚϵķ����Լ������뷽��֮��Ĺ�ϵ�����������Ѷȵ���Ŀ.�ڽ������С�Ƚϵ���Ŀʱ���������ȸ��ݷ��̵�˼��ó����������Ľ������꣬Ȼ���������x��Ĵ��ߣ�Ȼ����ݺ���������λ�ý��бȽϴ�С�ó��𰸣���������x��Գƣ���������������Ϊ�෴�������ڷ������ı䣬���ڴ�С���ı䣻����ֱ�����������Ƿ��н���ʱ���������ɷ��̣�Ȼ�����һԪ���η��̸����б�ʽ�������ж�.
�����͡������
��������
17
ij�̼Ҿ���һ���̲裬����װ��������Ͷ��3000Ԫ����֪�̲�ÿǧ�˳ɱ�50Ԫ�����о���������y��kg�������۵���x��Ԫ/ kg���ı仯���仯������仯�������±���ʾ��

����̲������������Ϊw��Ԫ�������������ۡ����������ɱ���
��1��������ϱ������y��x֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ����
��2����w��x֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ���������xΪ��ֵʱ��w��ֵ���
��3�����ڵ�һ�������ʹw������ֵ�����۵��۽������ۺ��ڵڶ�����������۲��Ÿ�Ԥ�����۵��۲��ø���80Ԫ��Ҫ����ȫ���ջ�װ��Ͷ�ʵĻ�����ʹ�ڶ����µ��������ٴﵽ1700Ԫ����ô�ڶ�����ʱ��Ӧ��ȷ�����۵�����ʲô��Χ�ڣ�
��1���� ��2������ʱ�� �� ��3�������۵���ΪԪʱ����ȫ���ջ�Ͷ�ʵĻ�����ʹ�ڶ����µ�������1700Ԫ. ���������������������1�����ݱ��������.�����۵���ÿ����5Ԫ���������½�10Kg����w��x��һ�κ����������裬����70��100������75��90��������ʽ�ã� ��ã� ���� ��2����������=��λ����������������������� ����Ϊ����ʽ�ã� ����ʱ�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
������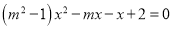 �ǹ���x��һԪһ�η��̣������ʽ|m��1|��ֵΪ����
�ǹ���x��һԪһ�η��̣������ʽ|m��1|��ֵΪ����
A. 0 B. 2 C. 0��2 D. ��2
A ������������һԪһ�η��̵Ķ��壬��m2-1=0����-m-1��0�� ��m2=1����m��-1�� ��m=1�� ��|m��1|=|1��1|=0. ��ѡA.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com