
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:单选题
用代数式表示“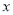 的3倍与
的3倍与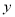 的平方的和”,正确的是( )
的平方的和”,正确的是( )
A. 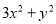 B.
B. 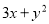 C.
C. 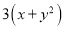 D.
D. 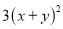
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
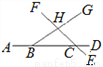
如图所示,其中共有________对对顶角.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
如图,已知抛物线y=x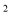 -ax+a
-ax+a -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
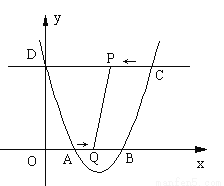
(1)求a的值;(2)当四边形ODPQ为矩形时,求这个矩形的面积;(3)当四边形PQBC的面积等于14时,求t的值.(4)当t为何值时,△PBQ是等腰三角形?(直接写出答案)
(1)8(2)(3)(4) 【解析】【解析】 (1)∵抛物线y=x-ax+a-4a-4经过点(0,8) ∴a-4a-4=8 解得:a=6,a=-2(不合题意,舍去) ∴a的值为6 (2)由(1)可得抛物线的解析式为 y=x-6x+8 当y=0时,x-6x+8=0 解得:x=2,x=4 ∴A点坐标为(2,0),B点坐标为(4,0) 当y=...查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为 .
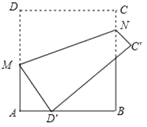
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列命题正确的个数有( )
①相等的圆周角所对的弧相等;②圆的两条平行弦所夹的弧相等;③三点确定一个圆;④在同圆或等圆中,同弦或等弦所对的圆周角相等或互补.
A. 1 B. 2 C. 3 D. 4
B 【解析】根据与圆有关的基本概念依次分析即可. ①在同圆或等圆中,相等的圆周角所对的弧相等故错误;②圆中两条平行弦所夹的弧相等,正确;③不在同一直线上的三点确定一个圆,故错误;④在同圆或等圆中,同弦或等弦所对的圆周角相等或互补,正确. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
下列运算正确的是
A.x•x2=x2 B.(xy)2=xy2 C.(x2)3=x6 D.x2+x2=x4
C 【解析】 试题分析:根据同底数幂的乘法,幂的乘方与积的乘方,合并同类项运算法则逐一计算作出判断: A、x•x2=x1+2=x3≠x2,故本选项错误; B、(xy)2=x2y2≠xy2,故本选项错误; C、(x2)3=x2×3=x6,故本选项正确; D、x2+x2=2x2=x4,故本选项错误。 故选C。查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
设a是方程x2﹣2006x+1=0的一个根,求代数式a2﹣2007a+ 的值.
的值.
【答案】-1
【解析】【试题分析】根据方程的根的定义,则x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,得a2﹣2007a+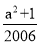 =
= .
.
【试题解析】
把x=a代入方程,可得:a2-2006a+1=0,
所以a2-2006a=-1,a2+1=2006a,
所以a2-2007a=-a-1,
所以a2-2007a+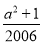 =-a-1+
=-a-1+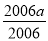 =-1,即a2-2007a+
=-1,即a2-2007a+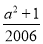 =-1.
=-1.
【方法点睛】本题目是一道考查一元二次方程的根的定义,方程的根满足该方程,代入得到相关代数式的值,进而将所求的额代数式进行转化,化简,求值.题目难度一般.
【题型】解答题
【结束】
5
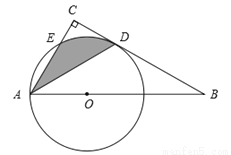
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:解答题
先化简再求值: 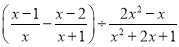 ,其中x=-3.
,其中x=-3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com