
如图,在Rt△ABC中,∠BAC=90°,∠C=30°
(1)请在图中用尺规作图的方法作出AC的垂直平分线交BC于点D,并标出D点 (不写作法,保留作图痕迹) .
(2)在(1)的条件下,连接AD,求证:△ABD是等边三角形.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源:山东省滨州市惠民县2017-2018学年八年级上学期期末数学试卷 题型:解答题
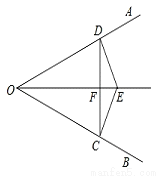
如图,已知点E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足.连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,求证:OE=4EF.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
若一个三角形三边a,b,c满足(a+b)2=c2+2ab,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 等腰直角三角形 D. 直角三角形
D 【解析】化简(a+b)2=c2+2ab,得,a2+b2=c2所以三角形是直角三角形, 故选:D.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:单选题
在下列说法中:
( )两点之间,直线最短.(
)两点之间,直线最短.( )两点之间的线段叫做这两点间的距离.(
)两点之间的线段叫做这两点间的距离.( )经过三个点中的任意两点画直线,可以画
)经过三个点中的任意两点画直线,可以画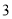 条直线.(
条直线.(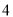 )
)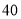 位同学,每两个同学之间互相送一份不同的纪念品,共需
位同学,每两个同学之间互相送一份不同的纪念品,共需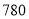 份纪念品.
份纪念品.
其中正确的说法共有( )
A. 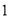 个 B.
个 B. 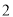 个 C.
个 C. 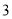 个 D.
个 D. 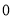 个
个
查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区安吉路实验学校2017-2018学年七年级上学期期中数学试卷 题型:单选题
用代数式表示:“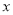 的5倍与
的5倍与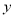 的和的一半”可以表示为( )
的和的一半”可以表示为( )
A.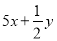 B.
B.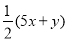 C.
C.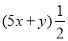 D.
D.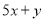
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:解答题
计算:(1)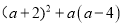 ; (2)
; (2)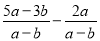 .
.
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:填空题
 =_______________.
=_______________.
查看答案和解析>>
科目:初中数学 来源:浙江省温州市2017-2018学年浙教版8年级上数学期末练习 题型:填空题
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则∠C=________.
90° 【解析】【解析】 设∠A=x,则∠B=2x,∠c=3x,∵x+2x+3x=180°,∴x=30°,∴∠C=3x=90°.故答案为:90°.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型:解答题
如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
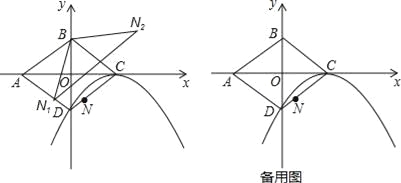
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
(1)y=﹣(x﹣2)2(2)证明见解析(3)(4) 【解析】试题分析:(1)用待定系数法求,即可; (2)由对称的特点得出∠N1BN2=2∠DBC结合菱形的性质即可; (3)先判定出,当BN⊥CD时,BN最短,再利用△ABC∽△N1BN2得到比例式,求解,即可; (4)先建立PE=m2﹣m+2函数解析式,根据抛物线的特点确定出最小值. 试题解析:(1)由已知,设抛物...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com