练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示的5个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿ADA1、A1EB1、B1FC1、C1GB的路线爬行，乙虫沿ACB的路爬行，则下列结论正确的是（  ）

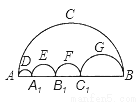
    A. 甲先到B点 B. 乙先到B点 C. 甲、乙同时到B点 D. 无法确定

    C 【解析】【解析】 π（AA1+A1B1+B1C1+C1B）=π×AB，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B点．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型：解答题

    某电动车厂一周计划生产2100辆电动车，平均每天计划生产300辆，由于各种原因，实际每天的生产量与计划量相比有出入．下表是某周的生产情况(超产为正，减产为负).

    星期

    一

    二

    三

    四

    五

    六

    日

    增减情况

    ＋5

    －2

    －4

    ＋13

    －10

    ＋16

    －9

    （1）根据记录可知本周前三天共生产电动车多少辆？

    （2）本周产量最多的一天比产量最少的一天多生产电动车多少辆？

    （3）该厂实行每周计件工资制，每生产一辆电动车可得a元，若超额完成，则超额部分每辆再奖b元(b＜a)，少生产一辆扣b元，求该厂工人这一周的工资总额.

    （注：第（1）、（2）小题列出算式，并计算）

    （1）899辆； （2）26辆；（3）(2109a+9b)元 【解析】（1）表示出三天的每一天生产的数量相加即可； （2）比较7个数据的大小，用最大的数据减去最小的数据即可； （3）算出一周的生产的总数量，与一周的计划产量相比写出代数式即可． 【解析】 （1）300×3+[(+5)+(-2)+(-4)]=899（辆）； （2）(+16)-(-10)=26（辆）； ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考数学二模试卷 题型：单选题

    某商店在节日期间开展优惠促销活动：购买原价超过200元的商品，超过200元的部分可以享受打折优惠．若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）的函数关系的图象如图所示，则超过200元的部分可以享受的优惠是（   ）

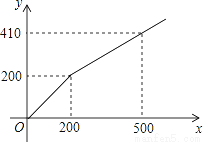
    A. 打八折 B. 打七折 C. 打六折 D. 打五折

    B 【解析】设， 把和代入， 得， ． ， ∴超过元部分打折． 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2018届九年级上期末模拟数学试卷 题型：填空题

    若⊙O的半径为6cm，则⊙O中最长的弦为 ________厘米．

    12 【解析】【解析】 ∵⊙O的半径为6cm，∴⊙O的直径为12cm，即圆中最长的弦长为12cm．故答案为：12．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2018届九年级上期末模拟数学试卷 题型：单选题

    一枚炮弹射出x秒后的高度为y米，且y与x之间的关系为y=ax2+bx+c（a≠0），若此炮弹在第3.2秒与第5.8秒时的高度相等，则在下列时间中炮弹所在高度最高的是（   ）

    A. 第3.3s B. 第4.3s C. 第5.2s D. 第4.6s

    D 【解析】【解析】 ∵炮弹在第3.2秒与第5.8秒时的高度相等， ∴抛物线的对称轴方程为x=4.5． ∵4.6s最接近4.5s，∴当4.6s时，炮弹的高度最高．故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2018届九年级上期中数学试卷 题型：解答题

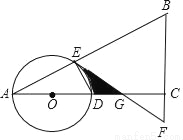
    如图，在△ABC中，∠ACB=90°，O是边AC上一点，以O为圆心，OA为半径的圆分别交AB，AC于点E，D，在BC的延长线上取点F，使得BF=EF，EF与AC交于点G．

    （1）试判断直线EF与⊙O的位置关系，并说明理由；

    （2）若OA=2，∠A=30°，求图中阴影部分的面积．

    （1）EF是⊙O的切线，理由见解析；（2）S阴影= ． 【解析】试题分析：（1）连接OE，根据等腰三角形的性质得到∠A=∠AEO，∠B=∠BEF，于是得到∠OEG=90°，即可得到结论；（2）由AD是⊙O的直径，得到∠AED=90°，根据三角形的内角和得到∠EOD=60°，求得∠EGO=30°，根据三角形和扇形的面积公式即可得到结论． 试题解析：（1）连接OE， ∵OA=OE，∴...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2018届九年级上期中数学试卷 题型：填空题

    过⊙O内一点M的最长弦为10cm，OM=3cm，则过M点的最短弦长是_____cm．

    8 【解析】根据垂径定理及勾股定理即可求出． 【解析】 由已知可知，最长的弦是过M的直径AB， 最短的是垂直平分直径的弦CD， 已知AB=10cm，OM=3cm， 则OD=5cm， 由勾股定理得MD=4cm， ∴CD=8cm， 故答案为8．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省海口市中考数学模拟试卷 题型：解答题

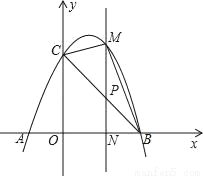
    如图，已知抛物线y=﹣x2+2x+3与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，连接BC．

    （1）求A，B，C三点的坐标；

    （2）若点P为线段BC上一点（不与B，C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当△BCM的面积最大时，求△BPN的周长；

    （3）在（2）的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在一点Q，使得△CNQ为直角三角形，求点Q的坐标．

    （1）A（﹣1，0），B（3，0），C（0，3）；（2）3+；（3）Q1（1， ），Q2（1， ），Q3（1，﹣），Q4（1， ）． 【解析】试题分析：（1）依据抛物线的解析式直接求得C的坐标，令y=0解方程即可求得A、B点的坐标； （2）求出△BCM面积的表达式，这是一个二次函数，求出其取最大值的条件；然后利用勾股定理求出△BPN的周长； （3）如解答图，△CNQ为直角三角形，...

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型：填空题

    按如图的程序计算，若开始输入的值x为正数，最后输出的结果为656，则满足条件的x的不同值最多有_______个．

    4 【解析】根据最后输出的结果，可计算出它前面的那个数，依此类推，可将符合题意的正数求出． 【解析】 ∵最后输出的数为656， ∴5x+1=656，得：x=131>0， ∴5x+1=131，得：x=26>0， ∴5x+1=26，得：x=5>0， ∴5x+1=5，得：x=0.8>0； ∴5x+1=0.8，得：x=?0.04<0，不符合题意， 故x的值...

    查看答案和解析>>

    同步练习册答案