练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

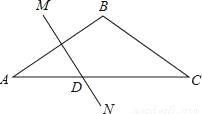
    如图，在△ABC中，BA=BC，∠B=120°，AB的垂直平分线MN交AC于D，求证：AD=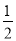DC．

    答案见解析 【解析】分析：连接BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出∠A=∠C=∠ABD=30°，再求出∠DBC=90°，再根据直角三角形30°所对的直角边等于斜边的一半即可得证． 本题解析: 如图，连接DB． ∵BA=BC，∠B=120°， ∴∠A=∠C=30°， ∵MN是AB的垂直平分线， ∴AD=DB， ∴...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：同步练习3：1.1菱形的性质与判定 题型：填空题

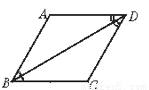
    若一条对角线平分平行四边形的一组对角，且一边长为a时，如图，其他三边长为__；周长为________.

    a 4a 【解析】因为一条对角线平分平行四边形的一组对角,所以可得平行四边形的邻边相等,即为菱形,故其它三边都为a,周长为4a,故答案为:a,4a.

    查看答案和解析>>

    科目：初中数学 来源：北师大版（贵州）八年级数学下册：期末综合检测 题型：单选题

    若x>y,则下列式子错误的是 (　　)

    A. x-3>y-3 B. -3x>-3y

    C. x+3>y+3 D. >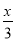

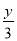
    B 【解析】A.把原不等式两边都减3，正确； B.把原不等式两边都乘以-3后，不等号要改变方向，错误； C.把原不等式两边都加3，正确； D.把原不等式两边都除以3，正确. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：浙江杭州西湖区第十三中学2017-2018学年八年级上学期中考试数学试卷（含解析） 题型：单选题

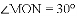
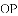
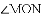
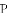
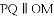
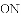
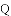
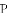
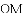
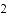
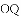
    如图，，且平分，过点作变于点，若点到的距离为，则的长为（ ）．

    A. B. C. D.

    A 【解析】 作PA⊥OM，PB⊥ON， ∵OP平分∠MON， ∴PA=PB=2，∠MOP=∠POQ=15°， ∵PQ∥OM， ∴∠MOP=∠OPQ=15°， ∴∠POQ=∠OPQ， ∴OQ=PQ，∠PQB=30°， ∴PQ=4， ∴OQ=4. 故选A.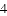

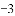
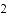
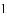
    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古呼和浩特市中考数学试卷六 题型：解答题

    阅读下列材料：

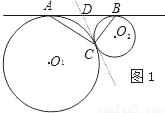
    如图1，⊙O1和⊙O2外切于点C，AB是⊙O1和⊙O2外公切线，A、B为切点，

    求证：AC⊥BC

    证明：过点C作⊙O1和⊙O2的内公切线交AB于D，

    ∵DA、DC是⊙O1的切线

    ∴DA=DC．

    ∴∠DAC=∠DCA．

    同理∠DCB=∠DBC．

    又∵∠DAC+∠DCA+∠DCB+∠DBC=180°，

    ∴∠DCA+∠DCB=90°．

    即AC⊥BC．

    根据上述材料，解答下列问题：

    （1）在以上的证明过程中使用了哪些定理？请写出两个定理的名称或内容；

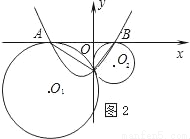
    （2）以AB所在直线为x轴，过点C且垂直于AB的直线为y轴建立直角坐标系（如图2），已知A、B两点的坐标为（﹣4，0），（1，0），求经过A、B、C三点的抛物线y=ax2+bx+c的函数解析式；

    （3）根据（2）中所确定的抛物线，试判断这条抛物线的顶点是否落在两圆的连心O1O2上，并说明理由．

    （1）见解析；（2） ；（3）见解析 【解析】试题分析：（1）由切线长相等可知用了切线长定理；由三角形的内角和是180°，可知用了三角形内角和定理； （2）先根据勾股定理求出点坐标，再用待定系数法即可求出经过三点的抛物线的函数解析式； （3）过作两圆的公切线，交于点，由切线长定理可求出点坐标，根据 两点的坐标可求出过两点直线的解析式，根据过一点且互相垂直的两条直线解析式的关系可求出过两圆...

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古呼和浩特市中考数学试卷六 题型：填空题

    将下列式子因式分【解析】
    x﹣x2﹣y+y2=_____．

    （x﹣y）（1﹣x﹣y） 【解析】试题解析： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古呼和浩特市中考数学试卷六 题型：单选题

    下列各图形中，是中心对称图形但不一定是轴对称图形的图形是（　　）

    A. 平行四边形 B. 菱形 C. 正方形 D. 等腰梯形

    A 【解析】试题解析：A. 平行四边形是中心对称图形，不是轴对称图形，故本选项正确； B. 菱形是中心对称图形，也是轴对称图形，故本选项错误； C. 正方形是中心对称图形，也是轴对称图形，故本选项错误； D. 等腰梯形不是中心对称图形，是轴对称图形，故本选项错误. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2016--2017学年度江西省赣县区第二学期期中考试七年级数学试卷 题型：解答题

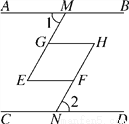
    如图是一个汉字“互”字，其中，AB∥CD，∠1＝∠2，∠MGH＝∠MEF.求证：∠MEF＝∠GHN.

    答案见解析 【解析】试题分析：延长ME交CD于P点，由AB//CD ，根据平行线的性质得∠1=∠3，而∠1=∠2，则∠2=∠3，可判断ME∥HN，根据平行线的性质得∠MGH=∠GHN，再由∠MGH=∠MEF，由等量代换 即可得到结论． 试题解析：延长ME交CD于点P, ∵AB//CD,∴∠1=∠3,又∵∠1=∠2,∴∠2=∠3,∴ME//HN ,∴∠MGH=∠GHN, 又∵...

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    已知：无论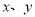取何值，多项式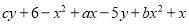： 的值不变.请回答问题：

    （1）请直接写出a、b、c的值： =　 　， =　 　， =　 　；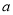

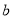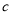    （2）数轴上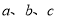三个数所对应的点分别为A、B、C，点A、B、C同时开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和4个单位长度的速度向右运动，假设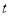秒钟过后，若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC．

    ①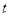秒钟过后，BC的长度为　 　（用含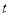的关系式表示）；

    ②请问：4AC﹣5AB的值是否随着时间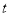的变化而改变？若变化，请说明理由；若不变，请求其值．

    (1)a=-1，b=1，c=5；(2)①t+4；②不变，4AC﹣5AB＝ 【解析】试题分析：（1）根据无论取何值，多项式： 的值不变,求出的值. （2）①先分别表示出秒钟过后的位置，根据数轴上两点之间的距离公式就可以求出结论； ②先根据数轴上两点之间的距离公式分别表示出和就可以得出的值的情况． 试题解析： 无论取何值，多项式： 的值不变, 解得： 故答案为：-...

    查看答案和解析>>

    同步练习册答案