练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知方程x2﹣3x+k=0有两个相等的实数根，则k=_____．

    【解析】∵x2﹣3x+k=0有两个相等的实数根， ∴△=， ∴9﹣4k=0， ∴k=． 故答案为．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省潍坊市诸城市2016-2017学年八年级（上）期末数学试卷 题型：单选题

    如图所示，有以下三个条件：①AC=AB，②AB∥CD，③∠1=∠2，从这三个条件中任选两个作为假设，另一个作为结论，则组成真命题的个数为（　　）

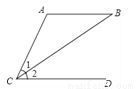
    A. 0 B. 1 C. 2 D. 3

    D 【解析】所有等可能的情况有3种，分别为①②⇒③；①③⇒②；②③⇒①，其中组成命题是真命题的情况有：①②⇒③；①③⇒②；②③⇒①， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：吉林省2017-2018学年度七年级数学上册期末测试卷 题型：填空题

    计算：15°37′+42°51′=_________．

    58°28′ 【解析】试题分析：先直接将度分秒相应位置上的数相加，再按满60进一的原则，向前进位即可． 试题解析：15°37′+42°51′=57°88′=58°28′．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

    ABCD中，E是CD边上一点，

    （1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是　 　，∠AFB=∠　 　

    （2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ；

    （3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2吗？

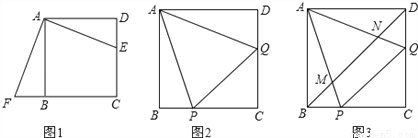
    （1）BF，AED；（2）证明见解析；（3）证明见解析. 【解析】试题分析：(1)、直接根据旋转的性质得到DE=BF，∠AFB=∠AED；(2)、将△ADQ绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABE，根据旋转的性质得∠EAQ=∠BAD=90°，AE=AQ，BE=DQ，而∠PAQ=45°，则∠PAE=45°，再根据全等三角形的判定方法得到△APE≌△APQ，则PE=PQ，于是...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

    如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为 ．

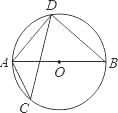
    65°． 【解析】试题分析：根据直径所对的圆周角是直角，构造直角三角形ABD，再根据同弧所对的圆周角相等，求得∠B的度数，即可求得∠BAD的度数． ∵AB为⊙O直径 ∴∠ADB=90° ∵相同的弧所对应的圆周角相等，且∠ACD=25° ∴∠B=25° ∴∠BAD=90°﹣∠B=65°．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：填空题

    如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是 _______

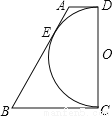
    14 【解析】试题分析：因为圆O与梯形上底AD、下底BC以及腰AB均相切，所以根据切线长定理可得AD=AE，BC=BE，又圆O的半径为2，梯形的腰AB为5，所以梯形的周长是5×2+4=14．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古乌兰察布市分校九年级（上）期中数学试卷 题型：单选题

    下列图形既是轴对称图形，又是中心对称图形的是（ ）

    A. 等边三角形 B. 平行四边形 C. 正五边形 D. 正方形

    D 【解析】试题分析：根据轴对称图形与中心对称图形的概念求解． 【解析】 A、是轴对称图形，不是中心对称图形．故错误； B、不是轴对称图形，是中心对称图形．故错误； C、是轴对称图形，不是中心对称图形．故错误； D、是轴对称图形，也是中心对称图形．故正确． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省白银市2018届九年级（上）期中数学试卷 题型：填空题

    如果x2-2（m+1）x+4是一个完全平方公式，则m= ．

    -3或1 【解析】 试题分析：∵x2-2（m+1）x+4是一个完全平方公式， ∴-2（m+1）=±4， 则m=-3或1．

    查看答案和解析>>

    科目：初中数学 来源：广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型：解答题

    有4个完全相同的小球，把它们分别标上数字﹣1，0，1，2，随机的摸出一个小球记录数字后放回摇匀，再随机的摸出一个小球记录数字，求两次摸球，球上标的数字都是正数的概率P（A）．

    【解析】试题分析：先画树状图得到所有可能出现的结果共有16种，两个数字都是正数的结果有4种，然后根据概率的定义即可得到两次都是正数的概率P（A）. 试题解析：画树状图， 所有可能出现的结果共有16种，每种结果出现的可能性都相同，两个数字都是正数的结果 有4种，所以P（A）=.

    查看答案和解析>>

    同步练习册答案