
在Rt△ABC中,∠C=900,∠B=2∠A,则cosB等于( )
A. 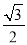 B.
B. 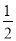 C.
C. 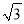 D.
D. 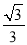
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:四川省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
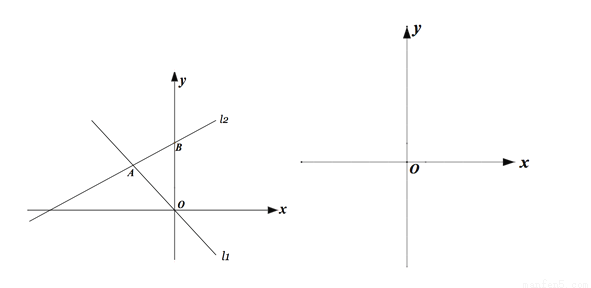
如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+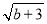 =0 .
=0 .
(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与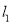 ,
, 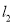 交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年七年级上学期期末数学试卷 题型:单选题
已知表示有理数a、b的点在数轴上的位置如图所示:

则下列结论正确的是
A. |a|<1<|b| B. 1<a<b C. 1<|a|<b D. -b<-a<-1
C 【解析】试题解析:∵由图可知,a<-1<1<b,1<|a|<b, ∴-b<a<-1,1<-a<b,故A、B、D错误,C正确. 故选C.查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:解答题
解方程:(1)(x+4)2=5(x+4); (2)2x2 -x -1=0.
(1) x1 =-4,x2=1 (2) x1 =-,x2=1 【解析】试题分析:(1)将方程右边的项移到方程左边,然后提取公因式x+4,得到(x+4)(x-1)=0,即可解出x;(2)利用十字相乘法将方程左边因式分解,解出x即可. 试题解析: (1)(x+4)2-5(x+4)=0, (x+4)(x-1)=0, x+4=0或x-1=0, 即x1=-4,x2=1; ...查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:填空题
若式子 在实数范围内有意义,则取值范围是________.
在实数范围内有意义,则取值范围是________.
查看答案和解析>>
科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:单选题
下列计算正确的是( )
A. 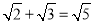 B.
B. 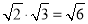 C.
C. 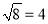 D.
D. 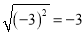
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:解答题
已知A=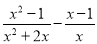 , B=2x2+4x+2.
, B=2x2+4x+2.
(1)化简A,并对B进行因式分解
(2)当B=0时,求A的值
(1),2(x+1)2;(2)﹣2 【解析】试题分析:(1)先根据分式混合运算的法则把A进行化简,对B进行因式分解即可; (2)根据B=0求出x的值,代入A式进行计算即可. 试题解析:(1)A= = = = =; B=2x2+4x+2=2(x2+2x+1)=2(x+1)2; (2)∵B=0,∴2(x+1)2=0, ∴x=﹣1. 当x...查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期检测八年级数学试卷 题型:单选题
分式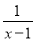 一定有意义,则x的取值范围是 ( )
一定有意义,则x的取值范围是 ( )
A. x〉1 B. x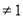 C. x<1 D. 一切实数
C. x<1 D. 一切实数
查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
等腰三角形一腰上的高与另一腰的夹角为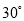 ,腰长为6,则其底边上的高是______.
,腰长为6,则其底边上的高是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com