练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列判断正确的是(　　)

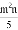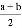    A. 3a2bc与bca2不是同类项 B. 和都是单项式

    C. 单项式－x3y2的次数是3，系数是－1 D. 3x2－y＋2xy2是三次三项式

    D 【解析】A.3a2bc与bca2是同类项，故错误； B.是多项式，故错误； C. 单项式－x3y2的次数是5，,系数是?1，故错误； D.3x2－y＋2xy2是三次三项式，故正确. 故选：D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省东营市河口区2017－2018学年度第一学期期末考试七年级数学试卷 题型：解答题

    为解决中小学大班额问题，东营市各县区今年将改扩建部分中小学，某县计划对A、B两类学校进行改扩建，根据预算，改扩建2所A类学校和3所B类学校共需资金7800万元，改扩建3所A类学校和1所B类学校共需资金5400万元.

    （1）改扩建1所A类学校和1所B类学校所需资金分别是多少万元？

    （2）该县计划改扩建A、B两类学校共10所，改扩建资金由国家财政和地方财政共同承担，若国家财政拨付资金不超过11800万元，地方财政投入资金不少于4000万元，其中地方财政投入到A、B两类学校改扩建资金分别为每所300万元和500万元，请问共有哪几种改扩建方案？

    （1）1200万元或1800万元；（2）有三种方案. 【解析】试题分析：（1）可根据“改扩建2所A类学校和3所B类学校共需资金7800万元，改扩建3所A类学校和1所B类学校共需资金5400万元”，列出方程组求出答案； （2）要根据“国家财政拨付资金不超过11800万元；地方财政投入资金不少于4000万元”来列出不等式组，判断出不同的改造方案． 试题解析：（1）设改扩建一所A类和一...

    查看答案和解析>>

    科目：初中数学 来源：广东省实验学校2017-2018学年八年级（上）期中数学试卷 题型：单选题

    如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要（　　）米．

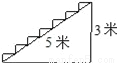
    A. 5 B. 7 C. 8 D. 12

    B 【解析】根据勾股定理求得楼梯的水平宽度==4，然后由地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和，地毯的长度至少是3+4=7米． 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：江西省赣州市2017-2018学年七年级（上）期中数学试卷 题型：解答题

    有理数a，b，c在数轴上的位置如图所示，且|a|=|c|．

    （1）若|a+c|+|b|=2，求b的值；

    （2）用“＞”从大到小把a，b，﹣b，c连接起来．

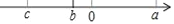
    (1)-2;(2)见解析. 【解析】试题分析：（1）由a、c之间的位置关系结合|a|=|c|可得出a+c=0，由b在数轴上的位置结合|a+c|+|b|=2可得出b的值； （2）将﹣b标记在数轴上，结合数轴即可得出a＞﹣b＞b＞c． 试题解析：【解析】 （1）∵|a|=|c|，且a，c分别在原点的两旁， ∴a，c互为相反数，即a+c=0． ∵|a+c|+|b|=2， ...

    查看答案和解析>>

    科目：初中数学 来源：江西省赣州市2017-2018学年七年级（上）期中数学试卷 题型：填空题

    已知关于x的方程（k﹣2）x|k|﹣1+5=3k是一元一次方程，则k=_____．

    -2 【解析】根据一元一次方程的解的定义，由关于x的方程（k﹣2）x|k|﹣1+5=3k是一元一次方程，可得|k|﹣1=1，且k﹣2≠0，解得k=﹣2． 故答案是：﹣2．

    查看答案和解析>>

    科目：初中数学 来源：吉林省辽源市东丰县2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图所示，E、F分别为线段AC上的两个点，且DE⊥AC于点E，BF⊥AC于点F，若AB=CD，AE=CF，BD交AC于点M．

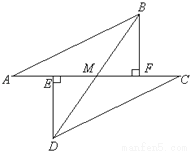
    （1）试猜想DE与BF的关系，并证明你的结论；

    （2）求证：MB=MD．

    （1）BF=DE；（2）证明见解析 【解析】 试题分析：（1）根据DE⊥AC，BF⊥AC可以证明DE∥BF；再求证Rt△ABF≌Rt△CDE可得BF=DE，即可解题； （2）根据（1）中结论可证△DEM≌△BFM，即可解题． 【解析】 （1）DE=BF，且DE∥BF， 证明：∵DE⊥AC，BF⊥AC， ∴∠DEC=∠BFA=90°． ∴DE∥BF， ...

    查看答案和解析>>

    科目：初中数学 来源：吉林省辽源市东丰县2017-2018学年八年级（上）期中数学试卷 题型：解答题

    如图，点B、D、C、F在一条直线上，且BD=FC，AB=EF．

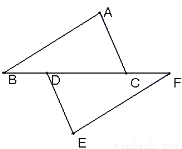
    （1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是 ；

    （2）添加了条件后，证明△ABC≌△EFD．

    （1）添加的条件是AC=ED； （2）∵点B、D、C、F在一条直线上，且BD=FC ∴BD+DC=CF+DC即BC=FD 在△ABC与△EFD 中 ∴△ABC≌△EFD 【解析】 试题分析：由BD=FC可得BC=FD，再有AB=EF，则可添加AC=ED根据“SSS”即可证得结论. （1）添加的条件是AC=ED； （2）∵点B、D、C、F在一条直线上，...

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

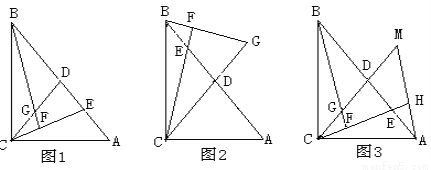
    已知：在△ABC中，AC=BC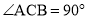， ，过点C作CD⊥AB于点D，点E是AB边上一动点（不同于点A、B），连接CE，过点B作CE的垂线交直线CE于点F，交直线CD于点G（如图1）.

    （1）求证：BG=CE；

    （2）若点E运动到线段BD上时（如图2），试猜想BG、CE的数量关系是否发生变化？请直接写出你的结论；

    （3）过点A作AH垂直于直线CE垂足为点H并交CD的延长线于点M（如图3），找出图中与BE相等的线段，并证明.

    （1）证明见解析；（2）不变，BG=CE；（3）BE=CM，理由见解析. 【解析】试题分析：（1）先由等边对等角得出∠ABC=∠CAB，再由同角的余角相等证得∠ACE=∠CBG，再由等腰直角三角形的性质得出∠A=∠BCD，由边角边可得△BCG≌△ACE，即可证得BG=CE； （2）如图②，根据等腰直角三角形的性质可以得出∠BCD=∠ACD=45°，根据直角三角形的三角形的性质就可以得出...

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市2016---2017初四中考调研检测数学试卷 题型：填空题

    函数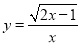的自变量x的取值范围为____________．

    x≥ 【解析】试题解析：根据题意得： 解得： 故答案为：

    查看答案和解析>>

    同步练习册答案