
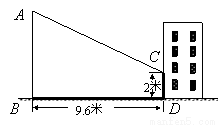
小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
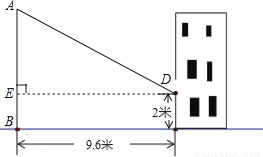
【答案】作DE⊥AB于点E,
根据题意得: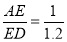 ,
,
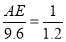 ,
,
解得:AE=8米.
则AB=AE+BE=8+2=10米.
即旗杆的高度为10米.
【解析】根据同一时刻物高与影长成正比,因而作DE⊥AB于点E,则AE与DE的比值,即同一时刻物高与影长的比值,即可求解.
【题型】解答题
【结束】
24
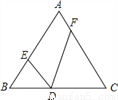
如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
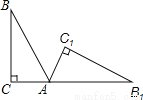
A. 55° B. 70° C. 125° D. 155°
C 【解析】根据直角三角形两锐角互余求出∠BAC,然后求出∠BAB′,再根据旋转的性质对应边的夹角∠BAB′即为旋转角. 【解析】 ∵∠B=35°,∠C=90°, ∴∠BAC=90°-∠B=90°-35°=55°, ∵点C、A、B1在同一条直线上, ∴∠BAB′=180°-∠BAC=180°-55°=125°, ∴旋转角等于125°. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
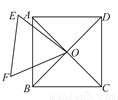
如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转.在旋转过程中,当AE=BF时,∠AOE的大小是__________.
查看答案和解析>>
科目:初中数学 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:填空题
在△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A=________°。
36° 【解析】如图 设∠A=x. ∵AD=BD, ∴∠ABD=∠A=x; ∵BD=BC, ∴∠BCD=∠BDC=∠ABD+∠A=2x; ∵AB=AC, ∴∠ABC=∠BCD=2x, ∴∠DBC=x; ∵x+2x+2x=180°, ∴x=36°, ∴∠A=36° 故答案为:36°.查看答案和解析>>
科目:初中数学 来源:人教版八年级上册数学第13章13.3《等腰三角形》 题型:单选题
已知∠AOB=30°,点P在∠AOB的内部,点P1与点P关于OB对称,点P2与点P关于OA对称,则以点P1,O,P2为顶点的三角形是( )
A. 直角三角形 B. 钝角三角形 C. 等腰三角形 D. 等边三角形
D 【解析】根据轴对称的性质,进行轴对称变换时对应线段相等,对应角相等, 即, ∠=∠, ∠=∠, 则∠=∠=2(∠BOP+∠POA)=2∠AOB=60°,已知两边相等且一个内角为60°的三角形为等边三角形,故选D.查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:解答题
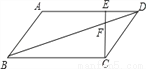
如图,在 ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
ABCD中,E为线段AD上一点,AE=4ED,CE、BD交于点F,若DF=4cm,则BF的长为 .
【答案】20
【解析】∵四边形ABCD是平行四边形,AE=4ED,
∴BC=AD=AE+ED=5ED,AD∥BC,
∴△DEF∽△BCF,
∴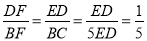 ,即
,即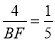 ,
,
∴BF=20.
【题型】填空题
【结束】
19
解方程:(1) 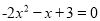 ; (2)
; (2)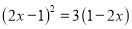 .
.
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:填空题
若一元二次方程x2-x-1=0的两根分别为x1,x2,则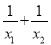 = .
= .
【答案】-1
【解析】∵一元二次方程: 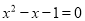 的两根是
的两根是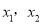 ,
,
∴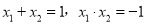 ,
,
∴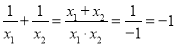 .
.
点睛:不解方程,求含有一元二次方程两根的代数式的值时,通常分两步完成:(1)由方程得到: 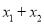 、
、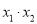 的值(前提是“根的判别式△
的值(前提是“根的判别式△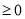 ”);(2)把要求值的代数式变形为用含“
”);(2)把要求值的代数式变形为用含“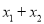 ”和“
”和“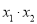 ”表达的形式,再代值计算即可.
”表达的形式,再代值计算即可.
【题型】填空题
【结束】
12
已知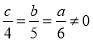 ,则
,则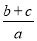 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
已知△ABC中,BC=8,BC上高h=4,D为BC上一点,EF∥BC,交AB于点E,交AC于点F(E、F不过A、B),设E到BC的距离为x,则△DEF的面积y关于x的函数图象大致为(如图所示)()
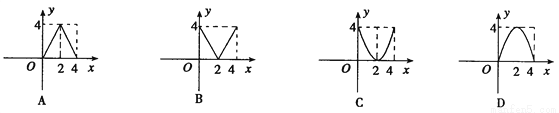
A. A B. B C. C D. D
D 【解析】过点A向BC作AH⊥BC于点H,所以根据相似比可知: , 即EF=,所以,故选D.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
有一辆载有长方体形状集装箱的货车想通横截面为抛物线的隧道,如图所示,已知隧道底部宽AB为 4 m,高OC为 3.2 m,集装箱的宽与货车的宽都是 2.4 m,集装箱顶部离地面 2.1 m.这辆货车能通过这个隧道吗?请说明理由.
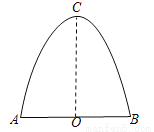
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com