练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    学校准确添置一批课桌椅原订购60套，每套72元，店方表示：如果多购可以优惠，结果校方购了72套，每套减价3元，但商店获得同样多的利润，求每套课桌椅成本.

    每套课桌椅成本54元. 【解析】试题分析：每套利润×套数=总利润，在本题中有两种方案，虽然单价不同，但是总利润相等，可依此列方程解应用题． 试题解析：设每套课桌椅成本元， 由题意得： ， 解得， 经检验，符合题意， 答：每套课桌椅成本54元.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

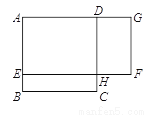
    在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图，自建房占地是边长为8m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG = 2BE. 如果设BE的长为x（单位：m），绿地AEFG的面积为y（单位：m2），那么y与x的函数的表达式为__________________；当BE =______m时，绿地AEFG的面积最大.

    2 【解析】由题意可知：AE=AB-BE=8-x，DG=2BE=2x，所以AG=AD+DG=8+2x， ∴y=AE·AG=（8-x）(8+2x)=-2x2+8x+64(0

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期期末考试数学试卷 题型：解答题

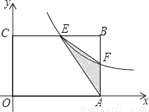
    如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数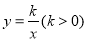的图象与BC边交于点E.

    （1）当F为AB的中点时，求该函数的解析式；

    （2）当k为何值时，△EFA的面积最大，最大面积是多少？

    （1）该函数的解析式为y=（x＞0）；（2）当k=12时，S有最大值，S最大=3. 【解析】如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数 (k>0) 的图象与BC边交于点E. （1）当F为AB的中点时，求该函数的解析式； （2）当k为何值时，△EFA的面积最大，最大面积是多少？ 试题分析：（1）当F为AB的中点时，...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期期末考试数学试卷 题型：单选题

    如图，A、B两点在双曲线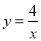的图象上，分别经过A、B两点向轴作垂线段，已知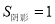，则（ ）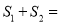

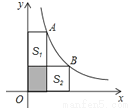
    A. 8 B. 6 C. 5 D. 4

    B 【解析】试题解析：∵点A、B是双曲线y=上的点，分别经过A、B两点向x轴、y轴作垂线段， 则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4， ∴S1+S2=4+4-1×2=6． 故选B.

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市2016-2017学年七年级下学期期末考试数学试卷 题型：解答题

    （1）如图1，在△ABC中∠A＝60 º，BD、CE均为△ABC的角平分线且相交于点O.

    ①填空：∠BOC＝ 度；

    ②求证：BC＝BE+CD．(写出求证过程)

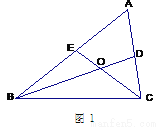
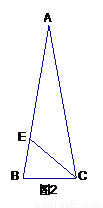
    （2）如图2，在△ABC中，AB=AC=m，BC=n， CE平分∠ACB．

    ①若△ABC的面积为S，在线段CE上找一点M，在线段AC上找一点N，使得AM+MN的值最小，则AM+MN的最小值是　　 　　　　．(直接写出答案)；　

    ②若∠A=20°，则△BCE的周长等于　　　　　　．(直接写出答案)．

    （1）①120；②证明见解析；（2）① (或)；②m 【解析】试题分析：（1）①根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB，则2∠BOC=360°-2∠OBC-2∠OCB，再根据角平分线的定义得∠ABC=2∠OBC，∠ACB=2∠OCB，则2∠BOC=360°-∠ABC-∠ACB，易得∠BOC=90°+∠A，由∠A＝60 º即可得∠BOC的值； ②采用截长法在在BC...

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市2016-2017学年七年级下学期期末考试数学试卷 题型：填空题

    把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起，则∠AEG的度数是_________

    81° 【解析】正五边形的内角的度数是×(5?2)×180°=108°， 正方形的内角是90°， 则∠EAG=108°?90°=18°， ∵AE=AG, ∴∠AEG=∠AGE= (180°-18°)=81°. 故答案为：81°.

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市2016-2017学年七年级下学期期末考试数学试卷 题型：单选题

    能够铺满地面的正多边形组合是( )

    A. 正五边形和正方形 B. 正八边形和正方形 C. 正六边形和正方形 D. 正十边形和正方形

    B 【解析】A.正五边形每个内角是180°?360°÷5=108°，正方形的每个内角是90°，108m+90n=360，n=4?m，显然m取任何正整数时，n不能得正整数，故不能铺满； B.正八边形的每个内角是135°，正方形的每个内角是90°，135m+90n=360，m=2时，显然n=1，故能铺满； C.正方形的每个内角是90°,正六边形的每个内角是120度.90m+120n=...

    查看答案和解析>>

    科目：初中数学 来源：四川省自贡市2017－2018学年上学期七年级期末统一考试数学试卷 题型：解答题

    化简: .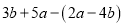

    【解析】试题分析：先去括号再合并同类项即可. 试题解析：原式==

    查看答案和解析>>

    科目：初中数学 来源：湖南省娄底市娄星区2017-2018学年九年级上学期期末考试数学试卷 题型：解答题

    为了巩固全国文明城市建设成果，突出城市品质的提升，近年来，我市积极落实节能减排政策，推行绿色建筑，据统计，我市2014年的绿色建筑面积约为950万平方米，2016年达到了1862万平方米．若2015年、2016年的绿色建筑面积按相同的增长率逐年递增，请解答下列问题：

    （1）求这两年我市推行绿色建筑面积的年平均增长率；

    （2）2017年我市计划推行绿色建筑面积达到2400万平方米．如果2017年仍保持相同的年平均增长率，请你预测2017年我市能否完成计划目标？

    (1) 年平均增长率为30%；(2) 2017年该市能完成计划目标. 【解析】试题分析：（1）根据题意可以列出相应的方程从而可以求得这两年我市推行绿色建筑面积的年平均增长率； （2）根据（1）中的增长率可以求得实际到2017年绿色建筑的面积，然后与计划的作比较，即可解答本题． 试题解析：（1）设这两年该市推行绿色建筑面积的年平均增长率为x， 700（1+x）2=1183 ...

    查看答案和解析>>

    同步练习册答案