
若不等式2x<4的解都能使关于x的一元一次不等式(a-1)x<a+5成立,则a的取值范围满足的不等式组是( )
A.  B.
B.  C.
C.  D.
D. 
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型:单选题
计算(a+b-c)(a-b-c)的结果是( )
A. a2-2ac+c2-b2 B. a2-b2+c2
C. a2-2ab+b2-c2 D. a2+b2-c2
A 【解析】试题解析:原式=[(a-c)+b][(a-c)-b] =(a-c)2-b2 =a2-2ac+c2-b2. 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018河北省保定市莲池区七年级第一学期数学期末试卷 题型:填空题
已知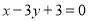 ,则
,则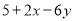 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:解答题
为支援某灾区,某市民政局组织募捐了240吨救灾物资,现租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
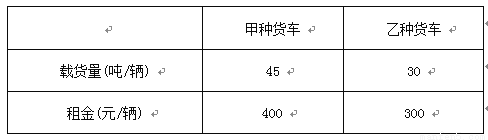
如果计划租用6辆货车,且租车的总费用不超过2 300元,求最省钱的租车方案.
租用甲种货车4辆,乙种货车2辆时最省钱. 【解析】试题分析:根据设租用甲种货车x辆,则租用乙种(6-x)辆,利用某市民政局组织募捐了240吨救灾物资,以及每辆货车的载重量得出不等式求出即可,进而根据每辆车的运费求出最省钱方案. 试题解析:设租甲种货车x辆,则租乙种货车(6-x)辆,依题意,得解得4≤x≤5,∵x为正整数,∴共有两种租车方案:①租甲种货车4辆,乙种货车2辆;②租甲种货车5...查看答案和解析>>
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:填空题
如图,直线y1=mx经过P(2,1)和Q(-4,-2)两点,且与直线y2=kx+b交于点P,则不等式kx+b>mx>-2的解集为_________________.
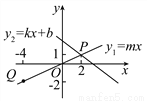
查看答案和解析>>
科目:初中数学 来源:2017-2018 北师大版数学八年级下册 第二章 一元一次不等式和一元一次不等式组 单元检测卷 题型:单选题
不等式组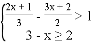 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A. 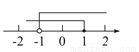
B. 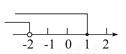
C. 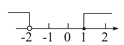
D. 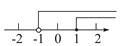
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:填空题
若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 ________
x<﹣3 【解析】根据不等式是一元一次不等式可得:2m+1=1且m?2≠0,∴m=0, ∴原不等式化为:?2x?1>5,解得x查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:单选题
某码头上有20名工人装载一批货物,已知每人往一艘轮船上装载2吨货物,装载完毕恰好用了6天,轮船到达目的地后,另一批工人开始卸货,计划平均每天卸货v吨,刚要卸货时遇到紧急情况,要求船上的货物卸载完毕不超过4天,则这批工人实际每天至少应卸货( )
A. 30吨 B. 40吨 C. 50吨 D. 60吨
D 【解析】设这批工人实际每天至少应卸货v吨, 根据题意得:2×6×20?4v, 解得:v?60, 故这批工人实际每天至少应卸货60吨; 故选:D.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:解答题
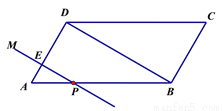
如图,在□ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截□ABCD所得图形的面积为S(cm2).求S关于t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com