
已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y2<y1 D. y2<y1<y3
C 【解析】由a<-1可得a-1<a<a+1<0,又因点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,在对称轴的左侧,y随x的增大而减小,所以 y3科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有__对.
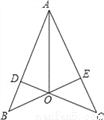
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:解答题
如图所示,矩形ABCD中,对角线AC、BD交于O点,CE⊥BD于E,OF⊥AB 于F,BE:DE=1:3,OF=2cm,求AC的长.
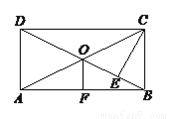
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:单选题
如果矩形ABCD的对角线AC和BD所成的锐角是60°,那么( ).
A. AC+BD=AB+BC+CD+DA B. BD=2AB
C. AC+BD=AB+BC D. 以上都不对
B 【解析】由矩形ABCD可得AC=BD,且AO=OC=OB=OD,AC和BD所成角为60°,可得AO=BO=CO=DO=AB=DC,只有B选项符合, 故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:解答题
已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=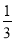 x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
(1);(2)2. 【解析】 试题分析:(1)将A、B的横坐标代入抛物线的解析式中,即可求得A、B的坐标,然后将它们代入直线的解析式中,可得方程组,解方程组即可求得a、b的值,从而得一次函数的表达式;(2)抛物线y=x2的顶点是原点O,设直线AB与x轴的交点为D,先根据直线AB的解析式求出D点坐标,然后根据△ADO的面积减去△OBD的面积=△OAB的面积即可求得. △OAB的面积...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:单选题
下列说法错误的是( )
A. 二次函数y=3x2中,当x>0时,y随x的增大而增大
B. 二次函数y=-6x2中,当x=0时,y有最大值0
C. a越大图象开口越小,a越小图象开口越大
D. 不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
C 【解析】试题解析:A、二次函数y=3x2图象开口向上,对称轴是y轴,当x>0时,y随x的增大而增大,正确; B、二次函数y=-6x2中开口向下,顶点(0,0),故当x=0时,y有最大值0,正确; C、|a|越大,图象开口越小,|a|越小图象开口越大,错误; D、抛物线y=ax2的顶点就是坐标原点,正确. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.2二次函数yax2的图象和性质 练习 题型:填空题
若函数y=(k2-4)x2+(k+2)x+3是二次函数,则k______.
k≠±2 【解析】∵函数y=(k2-4)x2+(k+2)x+3是二次函数, ∴,解得: .查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 25.1.1随机事件 测试 题型:填空题
如图,一个圆形转盘被等分成五个扇形区域,上面分别标有数字1、2、3、4、5,转盘指针的位置固定,转动转盘后任其自由停止.转动转盘一次,当转盘停止转动时,记指针指向标有偶数所在区域的概率为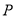 (偶数),指针指向标有奇数所在区域的概率为
(偶数),指针指向标有奇数所在区域的概率为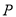 (奇数),则
(奇数),则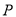 (偶数)
(偶数) 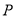 (奇数)(填“
(奇数)(填“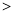 ”“
”“ 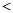 ”或“
”或“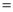 ”).
”).

查看答案和解析>>
科目:初中数学 来源:新人教版数学八年级上册第十三章轴对称13.1.2《线段的垂直平分线的性质》课时练习 题型:
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于D,若DE垂直平分AB,求∠B的度数.
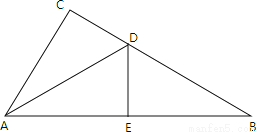
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com