
�����������������ĺͲ�����27�������������������У� ��
A. 3�� B. 4�� C. 5�� D. 6��
B ��������������������м������Ϊx����������������Ϊx-1��x+1�� ������ã�x+x-1+x+1��27�� ��ã�x��9�� ������������Ϊ���� ��x-1��0��x��0��x+1��0�� ��x��1�� ������x��ȡֵ��ΧΪ��1��x��9�� ��x��ȡ3��5��7��9��4�飮 ��ѡB��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����˽����֪˫��ѧУ2018����꼶���ϣ�������ѧģ���Ծ� ���ͣ������
һԪ���η���x��x��2��=x�ĸ���_____��
x1=0��x2=3 ���������������̣���x2��3x=0�� ��x��x��3��=0�� ���x1=0��x2=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³����۳���ѧ2018����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��ͼ���г�Ϊ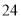 ����ʣ�һ������ǽ��ǽ�������ó���Ϊ
����ʣ�һ������ǽ��ǽ�������ó���Ϊ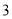 �ף���Χ��һ����������������ɵĻ��ԣ������Եı�
�ף���Χ��һ����������������ɵĻ��ԣ������Եı�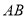 Ϊ__________��ʱ��Χ�ɵĻ���������������Ϊ__________ƽ���ף�
Ϊ__________��ʱ��Χ�ɵĻ���������������Ϊ__________ƽ���ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��ͼ����֪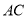 ƽ��
ƽ��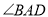 ��
�� 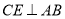 ��
��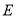 ��
�� 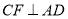 ��
��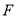 ����
����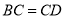 ��
��
��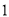 ����֤��
����֤�� 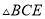 ��
��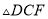 ��
��
��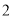 ����
����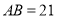 ��
�� 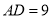 ��
�� 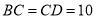 ����
����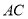 �ij���
�ij���
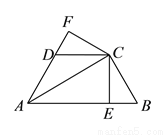
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��д�������������ε�������ȡ��������⣺__________��
����������ȵ��������ǵ��������� ����������ԭ����������ǣ���һ���������ǵ��������Ρ��������ǡ����������������ȡ��� �����⡰���������ε���������ȡ����������ǡ�����������ȵ��������ǵ��������Ρ��� �ʴ�Ϊ������������ȵ��������ǵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ���ѡ��
���и�ͼ�У���ȷ����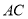 ���ϵĸߵ��ǣ� ����
���ϵĸߵ��ǣ� ����
A. 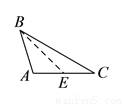 B.
B.  C.
C. 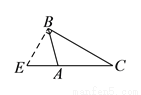 D.
D. 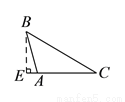
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ϲ���2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ����Ϊ7��6������������A��B��C���ڸ�㣨С�����εĶ��㣩�ϣ���ͼ��ȷ�����D��������һ����A��B��C��DΪ������ı��Σ�ʹ��������������������ͼ�λ�����ͬ����
��1����ͼ�����������ı����У���DΪ�۽ǣ����ı�������Գ�ͼ�Σ�
��2����ͼ�����������ı����У���DΪ��ǣ����ı��������ĶԳ�ͼ�Σ�
��3����ͼ���������ı����У���DΪֱ�ǣ����ı������Ϊ5ƽ����λ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ϲ���2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���x2��4x=0�ĸ��ǣ�������
A. 4 B. 0��4 C. ��4 D. 0�ͩ�4
B ���������������� x2��4x=0��x��x��4��=0����ã�x1=0��x2=4����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��ׯ��2017-2018ѧ����꼶���ϣ�������ѧ��ϰ�Ծ� ���ͣ���ѡ��
��֪��A��a��2016�����B����x��Գƣ���a+b��ֵΪ��������
A. ��1 B. 1 C. 2 D. 3
B ������������������ߵ����B����x��Գƣ� ��ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com