


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,某机器的油箱的容量为100升,机器的运行过程分为加油过程和加工过程,当油箱中的余油量为20升时,机器自动停止加工,进入加油过程直至加满,如此往复.图中的图象反应的是从最开始加油至第一个加工过程结束的情形.则下列结论中错误的( )
如图,某机器的油箱的容量为100升,机器的运行过程分为加油过程和加工过程,当油箱中的余油量为20升时,机器自动停止加工,进入加油过程直至加满,如此往复.图中的图象反应的是从最开始加油至第一个加工过程结束的情形.则下列结论中错误的( )| A、机器加油的速度为10升/分 | ||
B、机器在第一个加工过程中,油箱中的余油量y(升)与总运行时间x(分)的函数关系是y=-
| ||
| C、机器在第一个加工过程中,用时100分钟 | ||
| D、机器在加工过程中,每分钟耗油1升 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,矩形ABCD各顶点的坐标分别为A(-5,2)、B(-1,2)、C(-1,5)、D(-5,5).
如图,在平面直角坐标系中,矩形ABCD各顶点的坐标分别为A(-5,2)、B(-1,2)、C(-1,5)、D(-5,5).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一艘核潜艇在海面下300米的A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行1800米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(参考数据:
如图,一艘核潜艇在海面下300米的A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行1800米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度.(参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
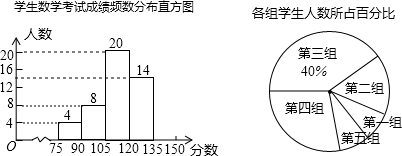
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com